
【题目】2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
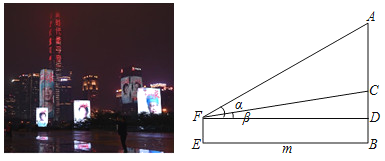
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O的半径为r,在射线OM上任取一点P(不与点O重合),如果射线OM上的点P',满足OP·OP'=r2,则称点P'为点P关于⊙O的反演点.

在平面直角坐标系xOy中,已知⊙O的半径为2.
(1)已知点A (4,0),求点A关于⊙O的反演点A'的坐标;
(2)若点B关于⊙O的反演点B'恰好为直线![]() 与直线x=4的交点,求点B的坐标;
与直线x=4的交点,求点B的坐标;
(3)若点C为直线![]() 上一动点,且点C关于⊙O的反演点C'在⊙O的内部,求点C的横坐标m的范围;
上一动点,且点C关于⊙O的反演点C'在⊙O的内部,求点C的横坐标m的范围;
(4)若点D为直线x=4上一动点,直接写出点D关于⊙O的反演点D'的横坐标t的范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
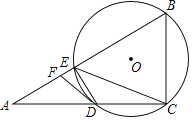
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AC上一点,过B,C,D三点的⊙O交AB于点E,连接ED,EC,点F是线段AE上的一点,连接FD,其中∠FDE=∠DCE.
(1)求证:DF是⊙O的切线.
(2)若D是AC的中点,∠A=30°,BC=4,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
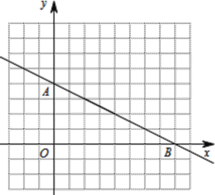
【题目】如图,单位长度为1的网格坐标系中,一次函数 ![]() 与坐标轴交于A、B两点,反比例函数
与坐标轴交于A、B两点,反比例函数![]() (x>0)经过一次函数上一点C(2,a).
(x>0)经过一次函数上一点C(2,a).
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个药店销售同一种口罩,在甲药店,不论一次购买数量是多少,价格均为3元/个;在乙药店,一次性购买数量不超过100个时,价格为3.5元/个;一次性购买数量超过100个时,其中100个的价格仍为3.5元/个,超过100个的部分的价格为2.5元/个.
(1)根据题意填表:
一次性购买数量(个) | 50 | 100 | 150 |
甲药店花费(元) |
| 300 |
|
乙药店花费(元) |
| 300 |
|
(2)当一次性购买多少个口罩时,在乙药店购买比在甲药店购买可以节约100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
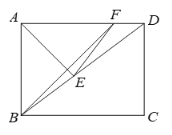
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上的一点,把△ABE沿着直线AE翻折得到△AFE,且点F恰好落在AD边上,连接BF.
(1)求△DEF的周长;
(2)求sin∠BFE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的曲边三角形可按下述方法作出:作等边三角形![]() ;分别以点
;分别以点![]() ,
,![]() ,
,![]() 为圆心,以
为圆心,以![]() 的长为半径作
的长为半径作![]() ,
,![]() ,
,![]() .三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为
.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为![]() ,那么这个曲边三角形的面积是___________.
,那么这个曲边三角形的面积是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
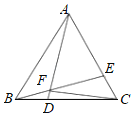
【题目】如图,在等边△ABC中,BD=CE,连接AD、BE交于点F.
(1)求∠AFE的度数;
(2)求证:ACDF=BDBF;
(3)连接FC,若CF⊥AD时,求证:BD=![]() DC.
DC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com