
����Ŀ����֪����ͼ����O�İ뾶Ϊr��������OM����ȡһ��P�������O�غϣ����������OM�ϵĵ�P'������OP��OP'=r2����Ƶ�P'Ϊ��P���ڡ�O�ķ��ݵ㣮

��ƽ��ֱ������ϵxOy�У���֪��O�İ뾶Ϊ2��
(1)��֪��A (4��0)�����A���ڡ�O�ķ��ݵ�A'�����ꣻ
(2)����B���ڡ�O�ķ��ݵ�B'ǡ��Ϊֱ��![]() ��ֱ��x=4�Ľ��㣬���B�����ꣻ
��ֱ��x=4�Ľ��㣬���B�����ꣻ
(3)����CΪֱ��![]() ��һ���㣬�ҵ�C���ڡ�O�ķ��ݵ�C'�ڡ�O���ڲ������C�ĺ�����m�ķ�Χ��
��һ���㣬�ҵ�C���ڡ�O�ķ��ݵ�C'�ڡ�O���ڲ������C�ĺ�����m�ķ�Χ��
(4)����DΪֱ��x=4��һ���㣬ֱ��д����D���ڡ�O�ķ��ݵ�D'�ĺ�����t�ķ�Χ��

���𰸡���1��A��(1��0)����2��B(![]() ��
��![]() )����3��m >1�� m <-1����4��0<t��1��
)����3��m >1�� m <-1����4��0<t��1��
��������
��1���ɷ��ݵ�Ķ������⣻
��2���������B'���꣬����OB'�ij����ɷ��ݵ�Ķ������OB�ij���������⣻
��3��������ɵ�OC'��2����OCOC'=4���ɵ�OC��2������C�ڡ�O���ⲿ��������⣻
��4��������ɵ�OD��4����ODOD'=4���ɵ�0��OD'��1��������⣮
��1���ߵ�A ��4��0����
��OA=4��
�ߵ�A'Ϊ��A���ڡ�O�ķ��ݵ㣬
��OAOA'=22=4��
��OA'=1��
��A'���꣨1��0����
��2����ͼ������B��BE��x���ڵ�E��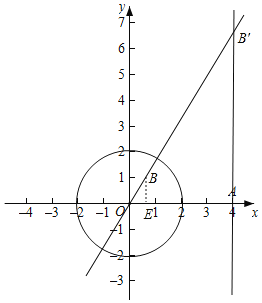
��B'ǡ��Ϊֱ��![]() ��ֱ��x=4�Ľ��㣬
��ֱ��x=4�Ľ��㣬
��![]() ��
��
�� ![]() ������Ϊ(4��
������Ϊ(4��![]() )��
)��
��OA=4��AB'=![]() ��
��
�� ![]() ��
��
��![]() ��
��
![]() ��
��
�ߵ�B'Ϊ��B���ڡ�O�ķ��ݵ㣬
��OBOB'=22=4��
��OB=![]() ��
��
�ߡ�OBE=90��-��BOE=30����
��![]() ��
��![]() ��
��
���B����Ϊ(![]() ��
��![]() )��
)��
��3���ߵ�CΪֱ��![]() ��һ���㣬�ҵ�C���ڡ�O�ķ��ݵ�C'�ڡ�O���ڲ���
��һ���㣬�ҵ�C���ڡ�O�ķ��ݵ�C'�ڡ�O���ڲ���
��![]() ��
��
��OCOC'=4��
��OC![]() ��
��
���C�ڡ�O���ⲿ��ֱ��![]() ���O��������������ĺ�����Ϊ
���O��������������ĺ�����Ϊ![]() ��
��
�� m��ȡֵ��Χ�� m >1�� m <-1��
��4���ߵ�DΪֱ��![]() ��һ���㣬
��һ���㣬
��OD��4��
��ODOD'=4��
��0��OD'��1��
��D'�ĺ�����t�ķ�Χ�ǣ�0��t��1��


 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪A��B���������ֱ�Ϊ��2![]() ��0������0��10����P�ǡ�AOB���Բ��C�ϵ�һ�㣬OP��AB�ڵ� D��
��0������0��10����P�ǡ�AOB���Բ��C�ϵ�һ�㣬OP��AB�ڵ� D��
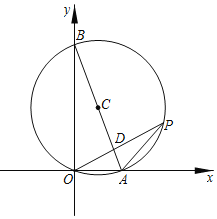
��1����OP��ABʱ����OP��
��2������AOP��30��ʱ����AP��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��
��![]() ���ۣ����Ϻ��ͼ����ͼ��ʾ����
���ۣ����Ϻ��ͼ����ͼ��ʾ����![]() ��
��![]() ������2�Ķ���Ϊ�� ��
������2�Ķ���Ϊ�� ��

A. 24�� B. 35�� C. 30�� D. 25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ο���ѧϰ�л��,��ʦ���������һ������:
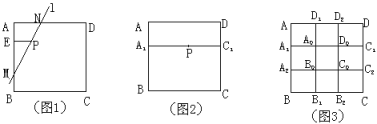
��P��������ABCD�ڵ�һ��,����P��ֱ��l�ֱ������ε������ڵ�M��N,ʹ��P���߶�MN�����ȷֵ�,������ֱ���ܹ�������?
����˼��,��ͬѧ�������»���:
��ͼ1,����P��PE��AB��E,��EB��ȡ��M,ʹEM=2EA,��ֱ��MP��AD��N,��ֱ��MN���Ƿ���������ֱ��l.
����������Ϣ,�����������:
(1)��ͬѧ�Ļ����Ƿ���ȷ?��˵������.
(2)��ͼ1��,�ܷ�������Ŀ������ֱ��?�����,��ֱ����ͼ1�л���.
(3)��ͼ2,A1��C1�ֱ���������ABCD�ı�AB��CD�ϵ����ȷֵ�,��A1C1��AD.����P���߶�A1C1��ʱ,�ܷ�������Ŀ������ֱ��?�����,���Ի�������?
(4)��ͼ3,������ABCD�߽��ϵ�A1��A2��B1��B2��C1��C2��D1��D2�������ڱߵ����ȷֵ�.����P��������ABCD�ڵIJ�ͬλ��ʱ,������,������Ŀ������ֱ��l�����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��
��![]() ��ͼ���ڵ�һ�����ڽ��ڵ�A�������A����ʱ��С�����ڿ�����k�����A��1 , 3����С�����ڿ�����m�����A��1,
��ͼ���ڵ�һ�����ڽ��ڵ�A�������A����ʱ��С�����ڿ�����k�����A��1 , 3����С�����ڿ�����m�����A��1, ![]() ����
����
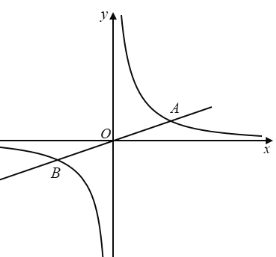
��1���������������Ĺ�ϵʽ����A�����ꣻ
��2�����ݺ���ͼ��ش���![]() ����ֱ��д��x��ȡֵ��Χ��
����ֱ��д��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB����O��ֱ������ABC�ڽ�����O����D����O�ϣ�ADƽ�֡�CAB��BC�ڵ�E��DF����O�����ߣ���AC���ӳ����ڵ�F��
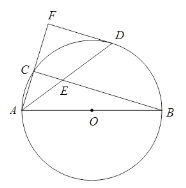
��1����֤��DF��AF��
��2������O�İ뾶��5�� AD=8����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ������ͣ�β�ͣѧ���ڼ���꼶ѧ��ƽ��ÿ��������ʱ���������ȡ��![]() �����꼶ѧ���������ʾ����飮���ĸ�ѡ�
�����꼶ѧ���������ʾ����飮���ĸ�ѡ�![]() Сʱ����)��
Сʱ����)��![]() Сʱ)��
Сʱ)��![]() Сʱ)��
Сʱ)�� ![]() Сʱ����)��ÿ��ֻ��ѡһ
Сʱ����)��ÿ��ֻ��ѡһ
��������������Ƴ����²�������ͳ�Ʊ���ͳ��ͼ��
������ѧ��ƽ��ÿ��������ʱ��ͳ�Ʊ�
ʱ�� | ��ռ�ٷֱ� |
|
|
|
|
|
|
|
|
�ϼ� |
|
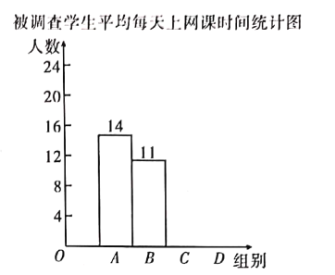
����������Ϣ������������⣺
![]() ��
��![]() ��
��
![]() ��ȫ����ͳ��ͼ��
��ȫ����ͳ��ͼ��
![]() ��У�о��꼶ѧ��
��У�о��꼶ѧ��![]() �������������У���꼶ѧ��ƽ��ÿ��������ʱ����
�������������У���꼶ѧ��ƽ��ÿ��������ʱ����![]() Сʱ�����ϵĹ���������
Сʱ�����ϵĹ���������
![]() �ڱ�����Ķ����У�ƽ��ÿ��ۿ�ʱ������
�ڱ�����Ķ����У�ƽ��ÿ��ۿ�ʱ������![]() Сʱ�ģ���
Сʱ�ģ���![]() �����Ծ�
�����Ծ�![]() �࣬
�࣬![]() �����Ծ�
�����Ծ�![]() �࣬������Ծ�
�࣬������Ծ�![]() �࣬�̵ֽ�������
�࣬�̵ֽ�������![]() ѡ������ѡ����ѧ�����е绰��̸�������б�������״ͼ�ķ���������ȡ��
ѡ������ѡ����ѧ�����е绰��̸�������б�������״ͼ�ķ���������ȡ��![]() ��ѧ��ǡ������ͬһ���༶�ĸ��ʣ�
��ѧ��ǡ������ͬһ���༶�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() �����ߣ���
�����ߣ���![]() ��
��![]() ���ӳ��߷ֱ��ڵ�
���ӳ��߷ֱ��ڵ�![]() ��
��![]() ������
������![]() ��
��
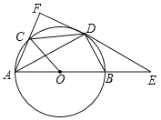
��1����֤��![]() ��
��
��2��ֱ�ӻش𣺢���֪![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��
������![]() ��
��![]() ��
��![]() ����
����![]() ���ڶ��ٶ�ʱ���ı���
���ڶ��ٶ�ʱ���ı���![]() �����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020��3��20�գ������������ļ��ܱ�¥��Ϊ���շ������ڵ�Ԯ��ҽ�ƶ�Ա���ƣ���ӭ���������ؼң�С���ڻ�ӭӢ�ۻؼ��ֳ�����ͼ�������۲Ӣ�ۻ������������A�͵�C�����Ƿֱ�Ϊ�����͡�����С����վλ��E����������ԵAC��ֱ�����B�����Ϊm�ף���ôӢ�ۻ����������ACΪ�� ��
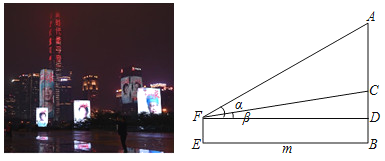
A.![]() ��B.mtan(������)��
��B.mtan(������)��
C.m(tan����tan��)��D.![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com