
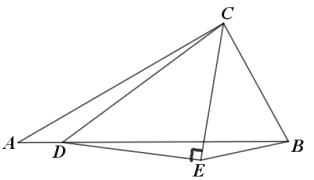
【题目】如图在![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 点沿线段
点沿线段![]() 向
向![]() 点运动,以
点运动,以![]() 为斜边在
为斜边在![]() 右侧作等腰直角三角形
右侧作等腰直角三角形![]() 则
则![]() 的最小值为_____________________.
的最小值为_____________________.
【答案】![]()
【解析】
以AC为斜边,在AC右侧作等腰直角三角形AE1C,边E1C与AB交与点G,连接E1E延长与AB交于点F,连接CF,作BE2⊥E1F于点E2.因为Rt△DCE与Rt△AE1C为等腰直角三角形,可得∠DCE=∠CDE=∠ACE1=∠CAE1=45°,于是∠ACD=∠E1CE,所以∠CAD=∠CE1E=30°,所以E在直线E1E上运动,当BE2⊥E1F时,BE最短,即为BE2的长.
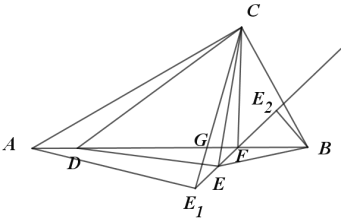
以AC为斜边,在AC右侧作等腰直角三角形AE1C,边E1C与AB交与点G,连接E1E延长与AB交于点F,连接CF,作BE2⊥E1F于点E2,因此△ACD∽△E1CE
∵Rt△DCE与Rt△AE1C为等腰直角三角形
∴∠DCE=∠CDE=∠ACE1=∠CAE1=45°
∴∠ACD=∠E1CE
∵![]()
∴△ACD∽△E1CE
∴∠CAD=∠CE1E=30°
∵D在AB上运动,
∴E在直线E1E上运动
当BE2⊥E1F时,BE最短,即为BE2的长
在△AGC与△E1GF中
∠AGC=∠E1GF,∠CAG=GE1F
∴∠GFE1=∠ACG=45°
∴∠CAD=∠CE1F=30°
∴点A,C,F,E1四点共圆
∴∠AE1C=∠ACF=90°,且∠ABC=60°,则∠BCF=30°
∵AC=6
∴BC=![]()
∴BF=![]()
∴BE2=![]()
故答案是![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
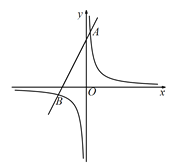
【题目】如图,函数![]() 与
与![]() 的图像在第一象限内交于点A,在求点A坐标时,小明由于看错了k,解得A(1 , 3);小华由于看错了m,解得A(1,
的图像在第一象限内交于点A,在求点A坐标时,小明由于看错了k,解得A(1 , 3);小华由于看错了m,解得A(1, ![]() ).
).
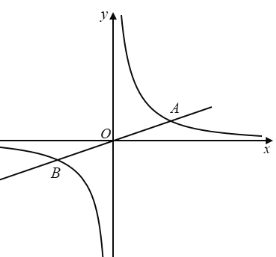
(1)求这两个函数的关系式及点A的坐标;
(2)根据函数图象回答:若![]() ,请直接写出x的取值范围.
,请直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
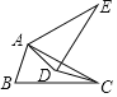
【题目】如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,若AB=2,∠ACB=30°,则线段CD的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
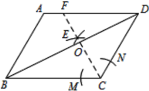
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步骤作图:①以C为圆心,以适当长为半径做弧,交CB、CD于M、N两点;②分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
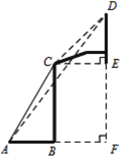
【题目】如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的C点观察篮板上沿D点的仰角为45°,在支架底端的A点观察篮板上沿D点的仰角为54°,点C与篮板下沿点E在同一水平线,若AB=1.91米,篮板高度DE为1.05米,求篮板下沿E点与地面的距离.(结果精确到0.1m,参考数据:sin54°≈0.80, cos54°≈0.60,tan54°≈1.33)

查看答案和解析>>
科目:初中数学 来源: 题型:
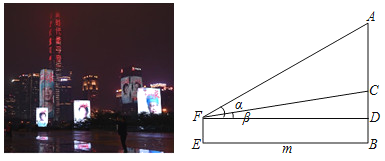
【题目】2020年3月20日,深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯,欢迎最美逆行者回家.小洪在欢迎英雄回家现场,如图,若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β,小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米,那么英雄画像电子屏高AC为( )
A.![]() 米B.mtan(α﹣β)米
米B.mtan(α﹣β)米
C.m(tanα﹣tanβ)米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
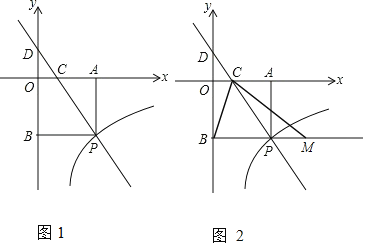
【题目】如图1,直线y1=kx+3与双曲线![]() (x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,
(x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,![]() .
.
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM,当△BCM为等腰三角形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面系中,一次函数![]() 的图像经过定点A,反比例函数
的图像经过定点A,反比例函数![]() 的图像经过点A,且与一次函数
的图像经过点A,且与一次函数![]() 的图像相交于点B(
的图像相交于点B(![]() ,m).
,m).
(1)求m、a的值;
(2)设横坐标为n的点P在反比例函数图象的第三象限上,且在点B右侧,连接AP、BP,△ABP的面积为12,求代数式![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简:![]() +
+![]() +…+
+…+![]() .
.
为了能找到复杂计算问题的结果,我们往往会通过将该问题分解,试图找寻算式中每个式子是否存在某种共同规律,然后借助这个规律将问题转化为可以解决的简单问题.下面我们尝试着用这个思路来解决上面的问题.请你按照这个思路继续进行下去,并把相应横线上的空格补充完整.
(分析问题)第1个加数:![]() =
=![]() ﹣
﹣![]() ;
;
第2个加数:![]() =
=![]() ﹣
﹣![]() ;
;
第3个加数:![]() =
=![]() ﹣
﹣![]() ;
;
第4个加数: =![]() ﹣
﹣![]() ;
;
(总结规律)第n个加数: = ﹣ .
(解决问题)请你利用上面找到的规律,继续化简下面的问题.(结果只需化简,无需求出最后得数)![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com