
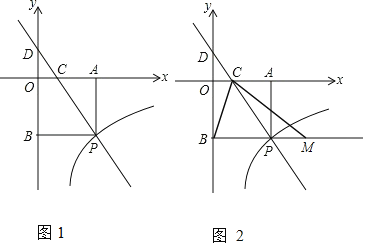
【题目】如图1,直线y1=kx+3与双曲线![]() (x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,
(x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,![]() .
.
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM,当△BCM为等腰三角形时,请直接写出点M的坐标.
【答案】(1)OD=3,AP=6;(2)m=4或9;(3)点M的坐标为(4,﹣6)或(10,﹣6)或(![]() ,﹣6)或(
,﹣6)或(![]() ,﹣6).
,﹣6).
【解析】
(1)设P(a,b),则OA=a,由![]() =
=![]() 得:C(
得:C(![]() a,0),由S△DBP=
a,0),由S△DBP=![]() ×DBBP=27,求出a值,进而求解;
×DBBP=27,求出a值,进而求解;
(2)将点P的坐标代入反比例解析式,即可求解;
(3)分BC=CM、BC=MB、MB=CM三种情况,分别求解即可.
解:(1)设P(a,b),则OA=a,
∵![]() =
=![]() ,
,
∴OC=![]() AC,
AC,
∴C(![]() a,0),
a,0),
∵点C在直线y=kx+3上,
∴0=![]() ak+3,即ka=﹣9,
ak+3,即ka=﹣9,
∴DB=3﹣b=3﹣(ka+3)=﹣ka=9,
∵BP=a,
∴S△DBP=![]() ×DBBP=27,
×DBBP=27,
∴![]() ×9a=27,
×9a=27,
∴a=6,
∴k=﹣![]() ,
,
∴一次函数的表达式为y=﹣![]() x+3;
x+3;
将x=6代入一次函数解析式得:y=﹣6,即P(6,﹣6),
∴AP=6,
由一次函数表达式得:点D(0,3),故OD=3;
(2)将点P的坐标代入反比例解析式得:m2﹣13m=﹣36,
解得:m=4或9;
(3)由(1)得,点Cspan>(2,0)、而点B(0,﹣6),设点M(m,﹣6);
则BC2=4+36=40,CM2=(m﹣2)2+36,MB2=m2,
当BC=CM时,40=(m﹣2)2+36,解得:m=4或0(舍去0);
当BC=MB时,同理可得:m=±![]() ;
;
当MB=CM时,同理可得:m=10,
故点M的坐标为(4,﹣6)或(10,﹣6)或(±![]() ,﹣6).
,﹣6).


科目:初中数学 来源: 题型:
【题目】下面是小东设计的“以线段AB为一条对角线作一个菱形”的尺规作图过程.
已知:线段AB.
求作:菱形ACBD.
![]()
作法:如图,
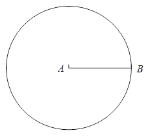
①以点A为圆心,以AB长为半径作⊙A;
②以点 B为圆心,以AB长为半径作⊙B,
交⊙A 于C,D两点;
③连接AC,BC,BD,AD.
所以四边形ACBD就是所求作的菱形.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵点B,C,D在⊙A上,
∴AB=AC=AD( )(填推理的依据).
同理 ∵点A,C,D在⊙B上,
∴AB=BC=BD.
∴ = = = .
∴四边形ACBD是菱形. ( )(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
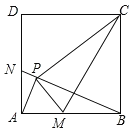
【题目】已知正方形ABCD的边长为1,点P为正方形内一动点,若点M在AB上,且满足△PBC∽△PAM,延长BP交AD于点N,连结CM.分析下列结论:①AP⊥BN;②BM=DN;③点P一定在以CM为直径的圆上;④正方形内不存在点P使得PC=![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
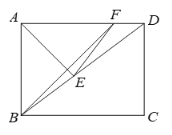
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是对角线BD上的一点,把△ABE沿着直线AE翻折得到△AFE,且点F恰好落在AD边上,连接BF.
(1)求△DEF的周长;
(2)求sin∠BFE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC=4,∠ACB=90°,D为边AB上一动点(不与A、B重合),⊙D与BC切于E点,E点关于CD的对称点F在△ABC的一边上,则BD=______.
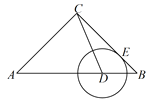
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
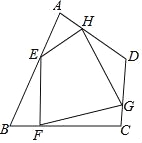
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
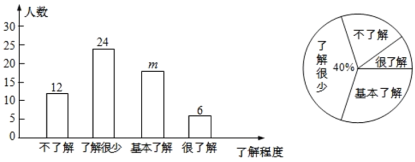
请你根据上面的信息,解答下列问题
(1)本次共调查了_______名员工,条形统计图中![]() ________;
________;
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数;
(3)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com