
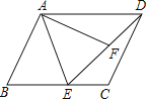
【题目】在平行四边形ABCD中,E是BC边上一点,F是DE上一点,若∠B=∠AFE,AB=AF.
求证:(1)△ADF≌△DEC.(2)BE=EF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据平行四边形的性质可得DC=AB,AD=BC,AB∥CD,然后再证明AF=DC,∠ADF=∠DEC,∠AFD=∠C,利用AAS可判定△ADF≌△DEC;
(2)根据全等三角形的性质得出AD=DE,DF=EC,再证出BC=DE,即可得出结论.
(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,AD=BC,AB∥CD,
∴∠ADF=∠DEC,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠B=∠AFE,
∴∠AFD=∠C,
∵AB=AF,
∴AF=DC,
在△ADF和△DEC中
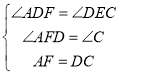 ,
,
∴△ADF≌△DEC(AAS);
(2)证明:∵△ADF≌△DEC,
∴AD=DE,DF=EC,
又∵AD=BC,
∴BC=DE,
∴BC-EC=DE-DF,
即BE=EF.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
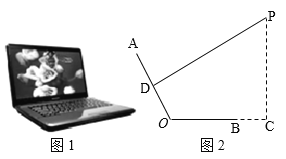
【题目】如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形.若显示屏AO与键盘BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,且PD⊥AO(此时点P为最佳视角),点C在OB的延长线上,PC⊥BC,BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)当∠AOC=115°时,线段PC的长比(1)中线段PC的长是增大还是减小?请通过计算说明.(结果精确到0.1cm,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
查看答案和解析>>
科目:初中数学 来源: 题型:
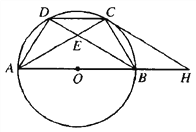
【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求![]() 之值;
之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=![]() ,求EC之长.
,求EC之长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,若AB=2,∠ACB=30°,则线段CD的长度为______.
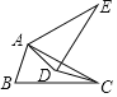
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
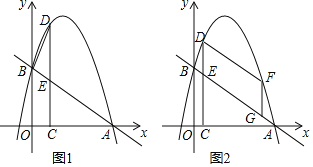
(1)求抛物线的函数表达式
(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;
(3)如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步骤作图:①以C为圆心,以适当长为半径做弧,交CB、CD于M、N两点;②分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
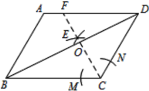
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一副篮架由配重、支架、篮板与篮筐组成,在立柱的C点观察篮板上沿D点的仰角为45°,在支架底端的A点观察篮板上沿D点的仰角为54°,点C与篮板下沿点E在同一水平线,若AB=1.91米,篮板高度DE为1.05米,求篮板下沿E点与地面的距离.(结果精确到0.1m,参考数据:sin54°≈0.80, cos54°≈0.60,tan54°≈1.33)

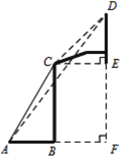
查看答案和解析>>
科目:初中数学 来源: 题型:
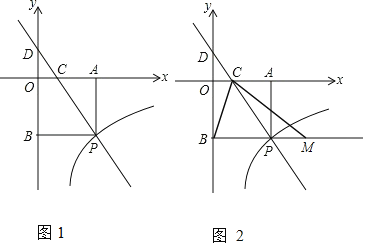
【题目】如图1,直线y1=kx+3与双曲线![]() (x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,
(x>0)交于点P,PA⊥x轴于点A,PB⊥y轴于点B,直线y1=kx+3分别交x轴、y轴于点C和点D,且S△DBP=27,![]() .
.
(1)求OD和AP的长;
(2)求m的值;
(3)如图2,点M为直线BP上的一个动点,连接CB、CM,当△BCM为等腰三角形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成,其比例与成本如下方表格所示,已知该饮料的成本价为8元/千克,按现价售出后可获利润50%,每个月可出售27500瓶.
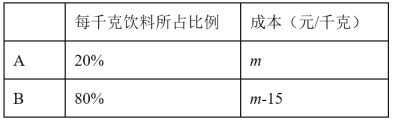
(1)求m的值;
(2)由于物价上涨,A水果成本提高了25%,B水果成本提高了20%,在不改变售价的情况下,若要保持每个月的利润不减少,则现在至少需要售出多少瓶饮料?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com