
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐyΘΫ©¹![]() x+3ΒΡΆΦœσ”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎBΒψΘ§≈ΉΈοœΏyΘΫ©¹x2+bx+cΨ≠ΙΐAΘ§BΝΫΒψΘ§‘ΎΒΎ“ΜœσœόΒΡ≈ΉΈοœΏ…œ»Γ“ΜΒψDΘ§ΙΐΒψDΉςDCΓΆx÷α”ΎΒψCΘ§ΫΜ÷±œΏAB”ΎΒψEΘ°
x+3ΒΡΆΦœσ”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎBΒψΘ§≈ΉΈοœΏyΘΫ©¹x2+bx+cΨ≠ΙΐAΘ§BΝΫΒψΘ§‘ΎΒΎ“ΜœσœόΒΡ≈ΉΈοœΏ…œ»Γ“ΜΒψDΘ§ΙΐΒψDΉςDCΓΆx÷α”ΎΒψCΘ§ΫΜ÷±œΏAB”ΎΒψEΘ°
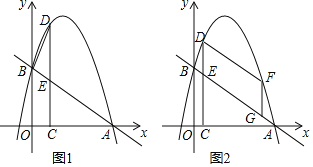
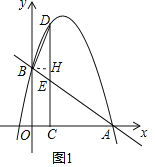
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο Ϋ
Θ®2Θ© «Ζώ¥φ‘ΎΒψDΘ§ ΙΒΟΓςBDEΚΆΓςACEœύΥΤΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψDΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
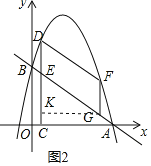
Θ®3Θ©»γΆΦ2Θ§F «ΒΎ“ΜœσœόΡΎ≈ΉΈοœΏ…œΒΡΕ·ΒψΘ®≤Μ”κΒψD÷ΊΚœΘ©Θ§ΒψG «œΏΕΈAB…œΒΡΕ·ΒψΘ°Ν§Ϋ”DFΘ§FGΘ§Β±ΥΡ±Ώ–ΈDEGF «ΤΫ––ΥΡ±Ώ–Έ«“÷ή≥ΛΉν¥σ ±Θ§«κ÷±Ϋ”–¥≥ωΒψGΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©yΘΫ©¹x2+![]() x+3ΘΜΘ®2Θ©¥φ‘ΎΘ°ΒψDΒΡΉχ±ξΈΣΘ®
x+3ΘΜΘ®2Θ©¥φ‘ΎΘ°ΒψDΒΡΉχ±ξΈΣΘ®![]() Θ§3Θ©ΜρΘ®
Θ§3Θ©ΜρΘ®![]() Θ§
Θ§![]() Θ©ΘΜΘ®3Θ©GΘ®
Θ©ΘΜΘ®3Θ©GΘ®![]() Θ§
Θ§![]() Θ©Θ°
Θ©Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί![]() Θ§«σ≥ωAΘ§BΒΡΉχ±ξΘ§‘Ό¥ζ»κ≈ΉΈοœΏΫβΈω Ϋ÷–Φ¥Ω…«σΒΟ≈ΉΈοœΏΫβΈω ΫΘΜ
Θ§«σ≥ωAΘ§BΒΡΉχ±ξΘ§‘Ό¥ζ»κ≈ΉΈοœΏΫβΈω Ϋ÷–Φ¥Ω…«σΒΟ≈ΉΈοœΏΫβΈω ΫΘΜ
Θ®2Θ©ΓςBDEΚΆΓςACEœύΥΤΘ§“ΣΖ÷ΝΫ÷÷«ιΩωΫχ––Χ÷¬έΘΚΔΌΓςBDEΓΉΓςACEΘ§«σΒΟ![]() Θ§
Θ§![]()
ΘΜΔΎΓςDBEΓΉΓςACEΘ§«σΒΟ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®3Θ©”…DEGF «ΤΫ––ΥΡ±Ώ–ΈΘ§Ω…ΒΟDEΓΈFGΘ§DE=FGΘ§…η![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΗυΨίΤΫ––ΥΡ±Ώ–Έ÷ή≥ΛΙΪ ΫΩ…ΒΟΘΚDEGF÷ή≥Λ=
Θ§ΗυΨίΤΫ––ΥΡ±Ώ–Έ÷ή≥ΛΙΪ ΫΩ…ΒΟΘΚDEGF÷ή≥Λ=![]() Θ§”…¥ΥΩ…«σΒΟΒψGΒΡΉχ±ξΘ°
Θ§”…¥ΥΩ…«σΒΟΒψGΒΡΉχ±ξΘ°
ΫβΘΚΘ®1Θ©‘Ύ![]() ÷–Θ§Νν
÷–Θ§Νν![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§Νν
Θ§Νν![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§
ΫΪ![]() Θ§
Θ§![]() Ζ÷±π¥ζ»κ≈ΉΈοœΏ
Ζ÷±π¥ζ»κ≈ΉΈοœΏ![]() ÷–Θ§ΒΟΘΚ
÷–Θ§ΒΟΘΚ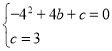 Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ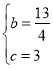 Θ§
Θ§
![]() ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚ
≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΈΣΘΚ![]() Θ°
Θ°
Θ®2Θ©¥φ‘ΎΘ°»γΆΦ1Θ§ΙΐΒψ![]() Ής
Ής![]() ”Ύ
”Ύ![]() Θ§…η
Θ§…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΘΜ
ΘΜ
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]()
![]() ΚΆ
ΚΆ![]() œύΥΤΘ§
œύΥΤΘ§![]()
![]() Μρ
Μρ![]()
ΔΌΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
![]()
![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]()
![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]()
ΔΎΒ±![]() ±Θ§
±Θ§![]()
![]()
![]() Θ§
Θ§
![]()
![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]()
![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ®…α
Θ®…α![]() Θ§
Θ§![]() Θ®…α
Θ®…α![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Ήέ…œΥυ ωΘ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§
Θ§![]() Μρ
Μρ![]() Θ§
Θ§![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦ3Θ§![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() «ΤΫ––ΥΡ±Ώ–Έ
«ΤΫ––ΥΡ±Ώ–Έ
![]() Θ§
Θ§![]()
…η![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
‘ρΘΚ![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]() Θ§
Θ§![]()
![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]()
ΙΐΒψ![]() Ής
Ής![]() ”Ύ
”Ύ![]() Θ§‘ρ
Θ§‘ρ![]()
![]()
![]()
![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]()
![]() Θ§Φ¥ΘΚ
Θ§Φ¥ΘΚ![]()
![]() ÷ή≥Λ
÷ή≥Λ![]()
![]() Θ§
Θ§
![]() Β±
Β±![]() ±Θ§
±Θ§![]() ÷ή≥ΛΉν¥σ÷Β
÷ή≥ΛΉν¥σ÷Β![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ≈ΉΈοœΏ±μ¥ο ΫCΘΚ![]() Θ§ “―÷ΣΒψA(0Θ§2)Θ§ΒψP «≈ΉΈοœΏ…œ“ΜΒψΘ§»τRtΓςAOP”–“ΜΗω»ώΫ«’ΐ«–÷ΒΈΣ
Θ§ “―÷ΣΒψA(0Θ§2)Θ§ΒψP «≈ΉΈοœΏ…œ“ΜΒψΘ§»τRtΓςAOP”–“ΜΗω»ώΫ«’ΐ«–÷ΒΈΣ![]() Θ§‘ρΒψPΒΡΉχ±ξ_________________Θ°
Θ§‘ρΒψPΒΡΉχ±ξ_________________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
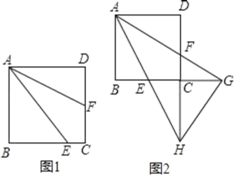
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCD÷–Θ§EΈΣBC±Ώ…œ»Έ“βΒψΘ§AFΤΫΖ÷ΓœEADΘ§ΫΜCD”ΎΒψFΘ°
(1)»γΆΦ1Θ§»τΒψF«ΓΚΟΈΣCD÷–ΒψΘ§«σ÷ΛΘΚAE=BE+2CEΘΜ
(2)‘Ύ(1)ΒΡΧθΦΰœ¬Θ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
(3)»γΆΦ2Θ§―”≥ΛAFΫΜBCΒΡ―”≥ΛœΏ”ΎΒψGΘ§―”≥ΛAEΫΜDCΒΡ―”≥ΛœΏ”ΎΒψHΘ§Ν§Ϋ”HGΘ§Β±CG=DF ±Θ§«σ÷ΛΘΚHGΓΆAGΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Αύ ΐ―ß–Υ»Λ–ΓΉιΕ‘Κ· ΐ![]() ΒΡΆΦœσΚΆ–‘÷ ΫΪΫχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘ°
ΒΡΆΦœσΚΆ–‘÷ ΫΪΫχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘ°
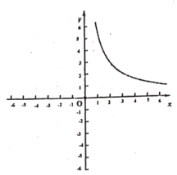
Θ®1Θ©Ή‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈß «≥ΐ0ΆβΒΡ»ΪΧε Β ΐΘ§
ΒΡ»Γ÷ΒΖΕΈß «≥ΐ0ΆβΒΡ»ΪΧε Β ΐΘ§![]() ”κ
”κ![]() ΒΡΦΗΉιΕ‘”Π÷ΒΝ–±μ»γœ¬ΘΚ
ΒΡΦΗΉιΕ‘”Π÷ΒΝ–±μ»γœ¬ΘΚ
| Γ≠ |
|
|
|
| 1 | 2 | 3 | 6 | Γ≠ |
| Γ≠ | 1 | 2 |
| 6 | 1 | 3 | 2 | 1 | Γ≠ |
Τδ÷–Θ§![]() _________Θ°
_________Θ°
Θ®2Θ©ΗυΨί…œ±μ ΐΨίΘ§‘Ύ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΟηΒψ≤ΔΜ≠≥ωΝΥΚ· ΐΆΦœσΒΡ“Μ≤ΩΖ÷Θ§«κΜ≠≥ωΗΟΚ· ΐΆΦœσΒΡΝμ“Μ≤ΩΖ÷Θ°
Θ®3Θ©Ιέ≤λΚ· ΐΆΦœσΘ§–¥≥ω“ΜΧθΚ· ΐ–‘÷ Θ°
Θ®4Θ©Ϋχ“Μ≤ΫΧΫΨΩΚ· ΐΆΦœσΖΔœ÷ΘΚ
ΔΌΚ· ΐΆΦœσ”κ![]() ÷αΫΜΒψ«ιΩω «________Θ§Υυ“‘Ε‘”ΠΖΫ≥Χ
÷αΫΜΒψ«ιΩω «________Θ§Υυ“‘Ε‘”ΠΖΫ≥Χ![]() ΒΡ Β ΐΗυΒΡ«ιΩω «________Θ°
ΒΡ Β ΐΗυΒΡ«ιΩω «________Θ°
ΔΎΖΫ≥Χ![]() ”–_______Ηω Β–ßΗυΘΜ
”–_______Ηω Β–ßΗυΘΜ
ΔέΙΊ”Ύ![]() ΒΡΖΫ≥Χ
ΒΡΖΫ≥Χ![]() ”–2Ηω Β ΐΗυΘ§
”–2Ηω Β ΐΗυΘ§![]() ΒΡ»Γ÷ΒΖΕΈß «________Θ°
ΒΡ»Γ÷ΒΖΕΈß «________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§’ΐΝυ±Ώ–ΈABCDEFΒΡΕ‘≥Τ÷––ΡP‘ΎΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσ…œΘ§±ΏCD‘Ύx÷α…œΘ§ΒψB‘Ύy÷α…œΘ°“―÷Σ
ΒΡΆΦœσ…œΘ§±ΏCD‘Ύx÷α…œΘ§ΒψB‘Ύy÷α…œΘ°“―÷Σ![]() Θ°
Θ°
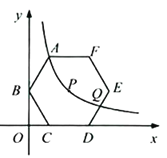
Θ®1Θ©ΒψA «Ζώ‘ΎΗΟΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘΩ«κΥΒΟςάμ”…Θ°
Θ®2Θ©»τΗΟΖ¥±»άΐΚ· ΐΆΦœσ”κDEΫΜ”ΎΒψQΘ§«σΒψQΒΡΚαΉχ±ξΘ°
Θ®3Θ©ΤΫ“Τ’ΐΝυ±Ώ–ΈABCDEFΘ§ ΙΤδ“Μ±ΏΒΡΝΫΗωΕΥΒψ«ΓΚΟΕΦ¬δ‘ΎΗΟΖ¥±»άΐΚ· ΐΒΡΆΦœσ…œΘ§ ‘Οη ωΤΫ“ΤΙΐ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
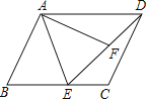
ΓΨΧβΡΩΓΩ‘ΎΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§E «BC±Ώ…œ“ΜΒψΘ§F «DE…œ“ΜΒψΘ§»τΓœB=ΓœAFEΘ§AB=AFΘ°
«σ÷ΛΘΚΘ®1Θ©ΓςADFΓ’ΓςDECΘ°Θ®2Θ©BE=EFΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
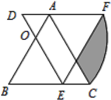
ΓΨΧβΡΩΓΩΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒψOΈΣAB±Ώ…œ“ΜΒψΘ§«“BO=2AO=4Θ§ΫΪΓςABC»ΤΒψOΡφ ±’κ–ΐΉΣ60ΓψΒΟΓςDEFΘ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ1Θ§ΒψPΈΣ’ΐΖΫ–ΈΡΎ“ΜΕ·ΒψΘ§»τΒψM‘ΎAB…œΘ§«“¬ζΉψΓςPBCΓΉΓςPAMΘ§―”≥ΛBPΫΜAD”ΎΒψNΘ§Ν§ΫαCMΘ°Ζ÷Έωœ¬Ν–Ϋα¬έΘΚΔΌAPΓΆBNΘΜΔΎBMΘΫDNΘΜΔέΒψP“ΜΕ®‘Ύ“‘CMΈΣ÷±ΨΕΒΡ‘≤…œΘΜΔή’ΐΖΫ–ΈΡΎ≤Μ¥φ‘ΎΒψP ΙΒΟPCΘΫ![]() Θ°Τδ÷–Ϋα¬έ’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
Θ°Τδ÷–Ϋα¬έ’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
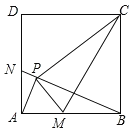
A.1ΗωB.2ΗωC.3ΗωD.4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΉι ΐΨίΘΚ3Θ§4Θ§4Θ§4Θ§5Θ°»τΡΟΒτ“ΜΗω ΐΨί4Θ§‘ρΖΔ…ζ±δΜ·ΒΡΆ≥ΦΤΝΩ «Θ® Θ©
A.ΦΪ≤νB.ΖΫ≤νC.÷–ΈΜ ΐD.÷Ύ ΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com