
【题目】抛物线表达式C:![]() , 已知点A(0,2),点P是抛物线上一点,若Rt△AOP有一个锐角正切值为
, 已知点A(0,2),点P是抛物线上一点,若Rt△AOP有一个锐角正切值为![]() ,则点P的坐标_________________.
,则点P的坐标_________________.
【答案】(-1,0)或(4,0)或(-4,2)
【解析】
由题意可知Rt△AOP中,分类讨论∠AOP=90°或∠PAO=90°,根据已知条件,P的横坐标可以是±1或±4,然后将P点坐标代入解析式中即可求得.
解:由题意可知Rt△AOP中,∠AOP=90°或∠PAO=90°,
∵抛物线![]() ,
,
∴抛物线开口向上,与x轴的交点为(-1,0)和(4,0),
当∠AOP=90°时,P点可能是(-1,0)或(4,0),
∴OP=1或4,
∵OA=2,且Rt△AOP有一个锐角正切值为![]() ,
,
∴OP=1或4
∴P点是(-1,0)或(4,0),
当∠OAP=90°时,P点纵坐标与A点纵坐标一样,把y=2代入![]() ,解得x=-4或7,
,解得x=-4或7,
∵OA=2,且Rt△AOP有一个锐角正切值为![]() ,
,
∴AP=1或4,
当AP=1时代入检验不满足一个锐角正切值为![]()
∴P点是(-4,2),
故答案为(-1,0)或(4,0)或(-4,2).


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C、点D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,连接AC、AD、BC,若∠ABD=2∠BDC.
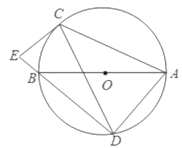
(1)求证:CE是⊙0的切线
(2)求证:△ABC![]() △CBE
△CBE
(3)若⊙O的半径为5,tan∠BDC=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个服装厂加工同种型号的防护服,甲厂每天加工的数量是乙厂每天加工数量的1.5倍,两厂各加工450套防护服,甲厂比乙厂要少用3天.
(1)求甲、乙两厂每天各加工多少套防护服?
(2)已知甲、乙两厂加工这种防护服每天的费用分别是180元和160元,疫情期间,某医院紧急需要2400套这种防护服,甲厂单独加工一段时间后另有安排,剩下任务只能由乙单独完成.如果总加工费不超过6000元,那么甲厂至少要加工多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
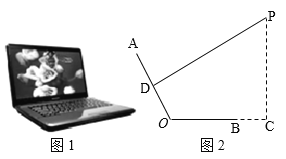
【题目】如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形.若显示屏AO与键盘BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,且PD⊥AO(此时点P为最佳视角),点C在OB的延长线上,PC⊥BC,BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)当∠AOC=115°时,线段PC的长比(1)中线段PC的长是增大还是减小?请通过计算说明.(结果精确到0.1cm,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() .
.
(1)当m=3时,求抛物线的顶点坐标;
(2)已知点A(1,2).试说明抛物线总经过点A;
(3)已知点B(0,2),将点B向右平移3个单位长度,得到点C,若抛物线与线段BC只有一个公共点,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,一次函数y=﹣![]() x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.
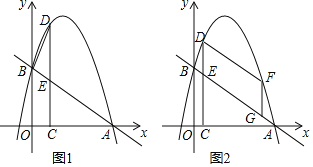
(1)求抛物线的函数表达式
(2)是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;
(3)如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com