
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
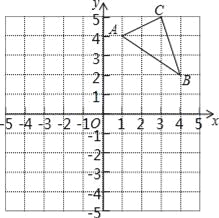
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如果把一个奇数位的自然数各数为上的数字从最高位到个位依次排列,与从个位到最高位依次排列出的一串数字完全相同,相邻两个数位上的数字之差的绝对值相等(不等于0),且该数正中间的数字与其余数字均不同,我们把这样的自然数称为“阶梯数”,例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,且|1﹣2|=|2﹣3|=|3﹣2|=|2﹣1|=1,因此12321是一个“阶梯数”,又如262,85258,…,都是“阶梯数”,若一个“阶梯数”t从左数到右,奇数位上的数字之和为M,偶数位上的数字之和为N,记P(t)=2N﹣M,Q(t)=M+N.
(1)已知一个三位“阶梯数”t,其中P(t)=12,且Q(t)为一个完全平方数,求这个三位数;
(2)已知一个五位“阶梯数”t能被4整除,且Q(t)除以4余2,求该五位“阶梯数”t的最大值与最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的新产品需要精加工后才能投放市场,为此王师傅承担了加工300个新产品的任务.在加工了80个新产品后,王师傅接到通知,要求加快新产品加工的进程,王师傅在保证加工零件质量的前提下,平均每天加工新产品的个数比原来多15个,这样一共用6天完成了任务.问接到通知后,王师傅平均每天加工多少个新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与X轴交点的横坐标分别为x1,x2,其中﹣2<x1<﹣1,0<x2<1,下列结论:
①4a﹣2b+c<0;②2a﹣b<0;③a+c<1;④b2+8a>4ac,
其中正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线![]() (x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )
(x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )

A. ![]() B.
B. ![]() C. 3 D. 6
C. 3 D. 6
【答案】A
【解析】试题分析:∵点D为平行四边形ABCO的对角线交点,双曲线y=![]() (x<0)经过点D,AC⊥y轴,
(x<0)经过点D,AC⊥y轴,
∴S平行四边形ABCO=4S△COD=4×![]() ×|
×|![]() |=
|=![]() .
.
故选A.
点睛:本题考查了反比例函数系数k的几何意义以及平行四边形的性质,根据平行四边形的性质结合反比例函数系数k的几何意义,找出S平行四边形ABCO=4S△COD=2|k|是解题的关键.
【题型】单选题
【结束】
9
【题目】如果分式![]() 在实数范围内有意义,则
在实数范围内有意义,则![]() 的取值范围是_____________.
的取值范围是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某集团决定购买![]() 、
、![]() 两种型号的污水处理设备共10台,其中每台价格及月处理污水量如下表:
两种型号的污水处理设备共10台,其中每台价格及月处理污水量如下表:
|
| |
价格(万元/元) | 15 | 12 |
处理污水量(吨/月) | 250 | 220 |
经预算,该集团准备购买设备的资金不高于130万元.
(1)请你设计该企业有哪几种购买方案?
(2)试通过计算,说明哪种方案处理污水多?
查看答案和解析>>
科目:初中数学 来源: 题型:
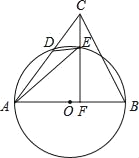
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在![]() 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4![]() ,cos∠ACF=
,cos∠ACF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com