
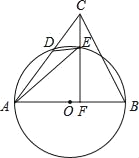
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在![]() 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4![]() ,cos∠ACF=
,cos∠ACF=![]() ,求EF的长.
,求EF的长.
【答案】(1)详见解析;(2)2![]() .
.
【解析】试题分析:(1)连接BD,由AB是 O的直径,得到∠ADB=90°,根据余角的性质得到∠CFA=180°-(DAB+∠3)=90°,于是得到结论;
(2)连接OE,由∠ADB=90°,得到∠CDB=180°-∠ADB=90°,根据勾股定理得到DB=![]() =8解直角三角形得到CD=4,根据勾股定理即可得到结论.
=8解直角三角形得到CD=4,根据勾股定理即可得到结论.
试题解析:(1)连接BD,

∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠1=90°,
∵∠1=∠2,∠2=∠3,
∴∠1=∠3,
∴∠DAB+∠3=90°,
∴∠CFA=180°﹣(DAB+∠3)=90°,
∴CF⊥AB;
(2)连接OE,
∵∠ADB=90°,
∴∠CDB=180°﹣∠ADB=90°,
∵在Rt△CDB中,CD=4,CB=4![]() ,
,
∴DB=![]() =8,
=8,
∵∠1=∠3,
∴cos∠1=cos∠3=![]() =
=![]() ,
,
∴AB=10,
∴OA=OE=5,AD=![]() =6,
=6,
∵CD=4,∴AC=AD+CD=10,
∵CF=ACcos∠3=8,
∴AF=![]() =6,
=6,
∴OF=AF﹣OA=1,
∴EF=![]() =2
=2![]() .
.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).
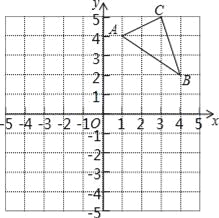
(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;
(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“非常时期,非常的爱”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.
请根据以上信息,解决下列问题:

(1)征文比赛成绩频数分布表中![]() 的值是_______,
的值是_______,![]() 的值是_______;
的值是_______;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=2x+4的图象与x、y轴分别相交于点A、B,四边形ABCD是正方形.
(1)求点A、B、D的坐标;
(2)求直线BD的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
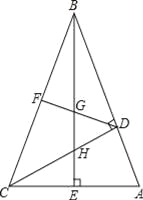
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市要对2.8万名初中生“学段人数分布情况”进行调查,采取随机抽样的方法从四个学年中抽取了若干名学生,并将调查结果绘制成了如下两幅不完整的条形统计图和扇形统计图,请根据图中提供的信息解答下列问题:

(1)在这次随机抽样中,一共调查了多少名学生?
(2)请通过计算补全条形统计图,并求出六年级所对应扇形的圆心角的度数;
(3)全市共有2.8万名学生,请你估计全市六、七年级的学生一共有多少万人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
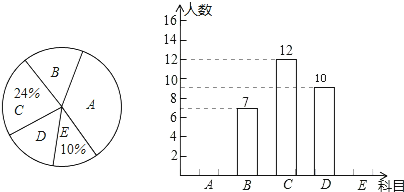
A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数占体育社团人数的一半
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
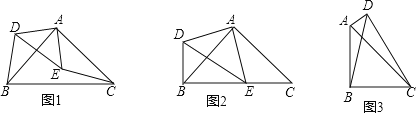
【题目】问题背景:某数学兴趣小组把两个等腰直角三角形的直角顶点重合,发现了一些有趣的结论.
结论一:
(1)如图1,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,连接BD,CE,试说明△ADB≌△AEC;
结论二:
(2)如图2,在(1)的条件下,若点E在BC边上,试说明DB⊥BC;
应用:
(3)如图3,在四边形ABCD中,∠ABC=∠ADC=90°,AB=CB,∠BAD+∠BCD=180°,连接BD,BD=7cm,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com