
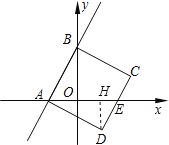
【题目】如图,一次函数y=2x+4的图象与x、y轴分别相交于点A、B,四边形ABCD是正方形.
(1)求点A、B、D的坐标;
(2)求直线BD的表达式.

【答案】(1)A(﹣2,0),点B(0,4),D(2,﹣2);(2)y=﹣3x+4.
【解析】
(1)由于ー次函数y=2x+4的图象与x、y轴分别相交于点A、B,所以利用函数解析式即可求出AB两点的坐标,然后过D作DH⊥x轴于H点,由四边形ABCD是正方形可以得到∠BAD=∠AOB=∠AHD=90°,AB=AD,接着证明△ABO≌△DAH,最后利用全等三角形的性质可以得到DH=AO=2,AH=BO=4,从而求出点D的坐标;
(2)利用待定系数法即可求解
解:(1)∵当y=0时,2x+4=0,x=﹣2.
∴点A(﹣2,0).
∵当x=0时,y=4.
∴点B(0,4).
过D作DH⊥x轴于H点,
∵四边形ABCD是正方形,
∴∠BAD=∠AOB=∠AHD=90°,AB=AD.
∴∠BAO+∠ABO=∠BAO+∠DAH,
∴∠ABO=∠DAH.
∴△ABO≌△DAH.
∴DH=AO=2,AH=BO=4,
∴OH=AH﹣AO=2.
∴点D(2,﹣2).
(2)设直线BD的表达式为y=kx+b.
∴![]()
解得![]() ,
,
∴直线BD的表达式为y=﹣3x+4.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】某课外学习小组在设计一个长方形时钟钟面时,欲使长方形的宽为20厘米,时钟的中心在长方形对角线的交点上,数字2在长方形的顶点上,数字3、6、9、12标在所在边的中点上,如图所示。
(1)问长方形的长应为多少?
(2)请你在长方框上点出数字1的位置,并说明确定该位置的方法;
(3)请你在长方框上点出钟面上其余数字的位置,并写出相应的数字(说明:要画出必要的、
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某集团决定购买![]() 、
、![]() 两种型号的污水处理设备共10台,其中每台价格及月处理污水量如下表:
两种型号的污水处理设备共10台,其中每台价格及月处理污水量如下表:
|
| |
价格(万元/元) | 15 | 12 |
处理污水量(吨/月) | 250 | 220 |
经预算,该集团准备购买设备的资金不高于130万元.
(1)请你设计该企业有哪几种购买方案?
(2)试通过计算,说明哪种方案处理污水多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简![]() .
.
解:将分子、分母同乘以![]() 得:
得:![]() .
.
类比应用:
(1)化简:![]() ;
;
(2)化简:![]() .
.
拓展延伸:
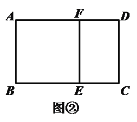
宽与长的比是![]() 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点B、C为线段AD上的两点,AB=![]() BC=
BC=![]() CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
CD,点E为线段CD的中点,点F为线段AD的三等分点,若BE=14,则线段EF=____________
查看答案和解析>>
科目:初中数学 来源: 题型:
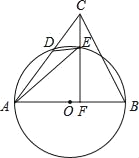
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在![]() 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4![]() ,cos∠ACF=
,cos∠ACF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”,这批单车分为A、B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动,投放A、B两种款型的单车共100辆,总价值36800元.求本次试点投放的A型车、B型车的辆数.
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A、B两车型的数量比进行投放,且投资总价值不低于184万元.问整个城区全面铺开时投放的A型车、B型车至少多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com