
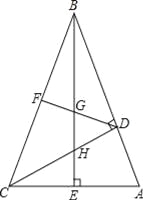
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2﹣GE2=EA2.
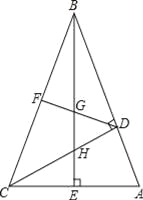
【答案】解:(1)线段BH与AC相等。证明如下:
∵∠BDC=∠BEC=∠CDA=90°,∠ABC=45°,
∴∠BCD=45°=∠ABC,∠A+∠DCA=90°,∠A+∠ABE=90°,
∴DB=DC,∠ABE=∠DCA,
在△DBH和△DCA中,∵∠DBH=∠DCA,BD=CD,∠BDH=∠CDA,
∴△DBH≌△DCA(ASA)。∴BH=AC。
(2)证明:连接CG,
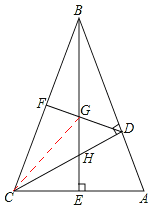
∵F为BC的中点,DB=DC,∴DF垂直平分BC。∴BG=CG。
∵∠ABE=∠CBE,BE⊥AC,∴∠AEB=∠CEB。
在△ABE和△CBE中,
∵∠AEB=∠CEB,BE=BE,∠CBE=∠ABE,
∴△ABE≌△CBE(ASA)。∴EC=EA。
在Rt△CGE中,由勾股定理得:CG2﹣GE2=EC2。
∴BG2﹣GE2=EA2。
【解析】试题分析:(1)、根据三角形的内角和定理求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根据ASA证出△DBH≌△DCA即可;(2)、根据DB=DC和F为BC中点,得出DF垂直平分BC,推出BG=CG,根据BE⊥AC和∠ABE=∠CBE得出AE=CE,在Rt△CGE中,由勾股定理即可推出答案.
试题解析:(1)、BH=AC,理由如下: ∵CD⊥AB,BE⊥AC, ∴∠BDH=∠BEC=∠CDA=90°, ∵∠ABC=45°,
∴∠BCD=180°﹣90°﹣45°=45°=∠ABC ∴DB=DC, ∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°, ∴∠HBD=∠ACD, ∵在△DBH和△DCA中
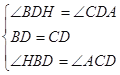 , ∴△DBH≌△DCA(ASA), ∴BH=AC.
, ∴△DBH≌△DCA(ASA), ∴BH=AC.
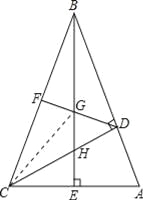
(2)、连接CG, 由(1)知,DB=CD, ∵F为BC的中点, ∴DF垂直平分BC, ∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC, ∴EC=EA, 在Rt△CGE中,由勾股定理得:CG2﹣GE2=CE2,
∵CE=AE,BG=CG, ∴BG2﹣GE2=EA2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某公司生产的新产品需要精加工后才能投放市场,为此王师傅承担了加工300个新产品的任务.在加工了80个新产品后,王师傅接到通知,要求加快新产品加工的进程,王师傅在保证加工零件质量的前提下,平均每天加工新产品的个数比原来多15个,这样一共用6天完成了任务.问接到通知后,王师傅平均每天加工多少个新产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
二次根式的除法,要化去分母中的根号,需将分子、分母同乘以一个恰当的二次根式.
例如:化简![]() .
.
解:将分子、分母同乘以![]() 得:
得:![]() .
.
类比应用:
(1)化简:![]() ;
;
(2)化简:![]() .
.
拓展延伸:
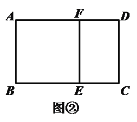
宽与长的比是![]() 的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
的矩形叫黄金矩形.如图①,已知黄金矩形ABCD的宽AB=1.
(1)黄金矩形ABCD的长BC= ;
(2)如图②,将图①中的黄金矩形裁剪掉一个以AB为边的正方形ABEF,得到新的矩形DCEF,猜想矩形DCEF是否为黄金矩形,并证明你的结论;

(3)在图②中,连结AE,则点D到线段AE的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有关于![]() ,
,![]() 的方程
的方程![]() .
.
(1)当![]() 和
和![]() 时,所得方程组成的方程组是
时,所得方程组成的方程组是![]() ,它的解是______;
,它的解是______;
(2)当![]() 和
和![]() 时,所得方程组成的方程组是______它的解是______;
时,所得方程组成的方程组是______它的解是______;
(3)猜想:无论![]() 取何值,关于
取何值,关于![]() ,
,![]() 的方程
的方程![]() 一定有一个解是______.
一定有一个解是______.
(4)猜想:无论![]() 取何值,关于
取何值,关于![]() ,
,![]() 的方程
的方程![]() 一定有一个解是______.
一定有一个解是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
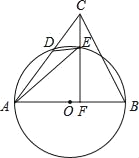
【题目】如图,在△ABC中,AB是⊙O的直径,AC与⊙O交于点D,点E在![]() 上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
上,连接DE,AE,连接CE并延长交AB于点F,∠AED=∠ACF.
(1)求证:CF⊥AB;
(2)若CD=4,CB=4![]() ,cos∠ACF=
,cos∠ACF=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
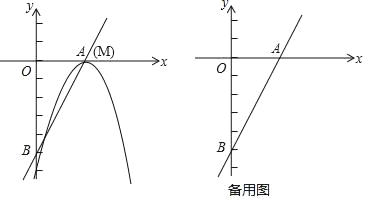
【题目】已知直线y=2x﹣5与x轴和y轴分别交于点A和点B,抛物线y=﹣x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=﹣x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:己知:对于实数a≥0,b≥0,满足a+b≥2![]() ,当且仅当a = b时,等号成立,此时取得代数式a+b的最小值.
,当且仅当a = b时,等号成立,此时取得代数式a+b的最小值.
根据以上结论,解决以下问题:
(1)拓展:若a>0,当且仅当a=___时,a+![]() 有最小值,最小值为____;
有最小值,最小值为____;
(2)应用:
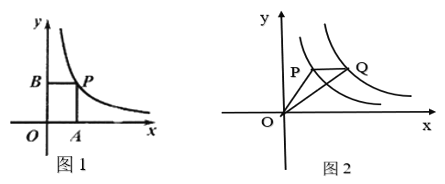
①如图1,已知点P为双曲线y=![]() (x>0)上的任意一点,过点P作PA⊥x轴,PB丄y轴,四边形OAPB的周长取得最小值时,求出点P的坐标以及周长最小值:
(x>0)上的任意一点,过点P作PA⊥x轴,PB丄y轴,四边形OAPB的周长取得最小值时,求出点P的坐标以及周长最小值:
②如图2,已知点Q是双曲线y=![]() (x>0)上一点,且PQ∥x轴, 连接OP、OQ,当线段OP取得最小值时,在平面内取一点C,使得以0、P、Q、C为顶点的四边形是平行四边形,求出点C的坐标.
(x>0)上一点,且PQ∥x轴, 连接OP、OQ,当线段OP取得最小值时,在平面内取一点C,使得以0、P、Q、C为顶点的四边形是平行四边形,求出点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com