
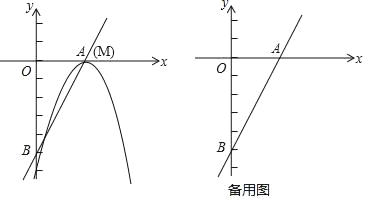
����Ŀ����ֱ֪��y=2x��5��x���y��ֱ��ڵ�A�͵�B��������y=��x2+bx+c�Ķ���M��ֱ��AB�ϣ�����������ֱ��AB����һ������ΪN��
��1����ͼ������M���A�غ�ʱ���������ߵĽ���ʽ��
��2���ڣ�1���������£����N��������߶�MN�ij���
��3��������y=��x2+bx+c��ֱ��AB��ƽ�ƣ��Ƿ���ڵ�M��ʹ����OMN����AOB���ƣ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=��x2+5x��![]() ����2��2
����2��2![]() ����3��M���������2����1����4��3����
����3��M���������2����1����4��3����
�������������������1�����������ֱ����x�ᣬy��Ľ������꣬���ö��κ����ĶԳ���Ĺ�ʽ������⣻
��N��ֱ����ͬʱ�ڶ��κ����ϣ������N�ĺ�������a���������������϶�Ӧ�ĵ����������ͬ���ݴ˼������a��ֵ����N�����꣬��N��NC��x�ᣬ����ΪC�����ù��ɶ����������MN�ij���
��2����AOB�����߳��������OB=2OA��AB���ϵĸ߿��������![]() ��������y=-x2+bx+c��ֱ��AB��ƽ�ƣ���MN�ij��Ȳ��䣬���ݣ�1���Ľ����2
��������y=-x2+bx+c��ֱ��AB��ƽ�ƣ���MN�ij��Ȳ��䣬���ݣ�1���Ľ����2![]() ��MN��AB���ϵĸߵĶ�������OM��AB��ON��ABʱ���������������ƣ��ݴ˼������M�����꣮
��MN��AB���ϵĸߵĶ�������OM��AB��ON��ABʱ���������������ƣ��ݴ˼������M�����꣮
�����������1���١�ֱ��y=2x-5��x���y�ύ�ڵ�A�͵�B��
��A(![]() ��0)��B��0��-5����
��0)��B��0��-5����
������M���A�غ�ʱ��
��M(![]() ��0)��
��0)��
�������ߵĽ���ʽ�ǣ�y��(x![]() )2����y��x2+5x
)2����y��x2+5x![]() ��
��
�ڡ�N��ֱ��y=2x-5�ϣ���N��a��2a-5������N��������y��x2+5x![]() �ϣ�
�ϣ�
��2a5��a2+5a![]() ��
��
���a1��![]() ��a2��
��a2��![]() ����ȥ��
����ȥ��
��N(![]() ��4)��
��4)��
��N��NC��x�ᣬ����ΪC��
��N(![]() ��4)��
��4)��
��C(![]() ��0)��
��0)��
��NC=4��MC��OMOC��![]()
![]() ��2��
��2��
��MN��![]() ��
��
��2����M��m��2m-5����N��n��2n-5����
��A(![]() ��0)��B��0��-5����
��0)��B��0��-5����
��OA=![]() ��OB=5����OB=2OA��AB=
��OB=5����OB=2OA��AB=![]() ��
��
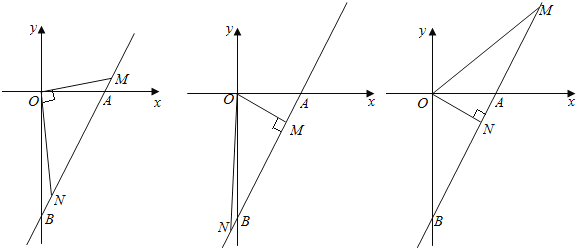
����MON=90��ʱ����AB��MN����MN��AB���ϵĸ���ȣ������OMN����AOB����ȫ�ȣ�
���OMN����AOB�����ƣ����������⣮
����OMN=90��ʱ�� ![]() ����
����![]() �����OM=
�����OM=![]() ��
��
��m2+��2m-5��2=��![]() ��2�����m=2��
��2�����m=2��
��M��2��-1����
����ONM=90��ʱ�� ![]() ����
����![]() �����ON=
�����ON=![]() ��
��
��n2+��2n-5��2=��![]() ��2�����n=2��
��2�����n=2��
��OM2=ON2+MN2��
��m2+��2m-5��2=5+��2![]() ��2��
��2��
���m=4��
��M��������M��4��3����
��M�������ǣ���2��-1����4��3����


 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90������CAD=30����AC=BC=AD��CE��CD����CE=CD������BD��DE��BE�������н��ۣ�����ECA=165������BE=BC����AD��BE����![]() =1��������ȷ���ǣ� ��
=1��������ȷ���ǣ� ��

A���٢ڢ� B���٢ڢ� C���٢ۢ� D���٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
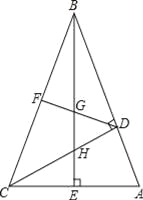
����Ŀ����ͼ������ABC�У���ABC=45����CD��AB��BE��AC������ֱ�ΪD��E��FΪBC�е㣬BE��DF��DC�ֱ��ڵ�G��H����ABE=��CBE��
��1���߶�BH��AC���������ȸ���֤�������������˵�����ɣ�
��2����֤��BG2��GE2=EA2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��ø��ƺ�����ˮ�ʣ����۹�˾��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±��������飺����һ̨A���豸�ȹ���һ̨B���豸��2��Ԫ������2̨A���豸�ȹ���3̨B���豸��6��Ԫ��
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
������ˮ������/�£� | 240 | 180 |
��1����a��b��ֵ��
��2�����۹�˾��Ԥ�㹺����ˮ�����豸���ʽ���105��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��3���ڣ�2���������£���ÿ��Ҫ������ˮ��������2040�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ḻѧ��������ijУ������չ���Ż��ѧ���ɸ����Լ��İ���ѡ��һ���֪��У��������������У�A������B������C������D����ë��E��ƹ��������ʦ��ij�꼶ͬѧѡ����������������е���ͳ�ƣ��Ƴ���������������ͳ��ͼ����ͼ���������½��۲���ȷ���ǣ� ��
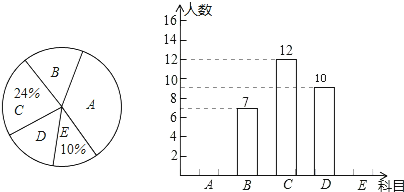
A��ѡ��ĿE����5��
B��ѡ��ĿD������Բ�Ľ���72��
C��ѡ��ĿA������ռ��������������һ��
D��ѡ��ĿB������Բ�ĽDZ�ѡ��ĿD������Բ�ĽǵĶ�����21.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �����ж�
�����ж�![]() ��
��![]() �Ĵ�С��ϵ����֤����Ľ��ۡ�
�Ĵ�С��ϵ����֤����Ľ��ۡ�
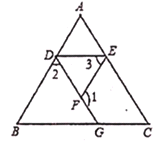
���룺��AED=��C��
���ɣ��ߡ�2+��ADF=180��( )��
��1+��2=180��( )��
���1=��ADF( )��
��AD��EF( )��
���3=��ADE( )��
�ߡ�3=��B( )��
���B=��ADE( )��
��DE��BC( )��
���AED=��C( )��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2��O3���� ���һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ��![]() ����λ���ȣ����2019��ʱ����P��������________________
����λ���ȣ����2019��ʱ����P��������________________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������D��BC�ϣ���E��AB�ϣ���DE��AC��AE=5��DE=2��DC=3������P�ӵ�A�������ر�AC��ÿ��2����λ�����ٶ����յ�C�˶���ͬʱ����F�ӵ�C���������߶�CD����ÿ��1����λ�����ٶ����յ�D�˶������˶�ʱ��Ϊt�룮
��1���߶�AC�ij�=________��
��2������PCF����EDF����ʱ����t��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com