
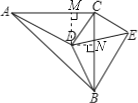
【题目】如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;④![]() =1.其中正确的是( )
=1.其中正确的是( )

A.①②③ B.①②④ C.①③④ D.①②③④
【答案】D
【解析】
试题分析:①根据:∠CAD=30°,AC=BC=AD,利用等腰三角形的性质和三角形内角和定理即可求出∠ECA=165°,从而得证结论正确;
②根据CE⊥CD,∠ECA=165°,利用SAS求证△ACD≌△BCE即可得出结论;
③根据∠ACB=90°,∠CAD=30°,AC=BC,利用等腰三角形的性质和△ACD≌△BCE,求出∠CBE=30°,然后即可得出结论;
④过D作DM⊥AC于M,过D作DN⊥BC于N.由∠CAD=30°,可得CM=![]() AC,求证△CMD≌△CND,可得CN=DM=
AC,求证△CMD≌△CND,可得CN=DM=![]() AC=
AC=![]() BC,从而得出CN=BN.然后即可得出结论.
BC,从而得出CN=BN.然后即可得出结论.
解:①∵∠CAD=30°,AC=BC=AD,∴∠ACD=∠ADC=![]() (180°﹣30°)=75°,
(180°﹣30°)=75°,
∵CE⊥CD,∴∠DCE=90°,
∴∠ECA=165°∴①正确;
②∵CE⊥CD,∠ECA=165°(已证),
∴∠BCE=∠ECA﹣∠ACB=165﹣90=75°,
∴△ACD≌△BCE(SAS),
∴BE=BC,∴②正确;
③∵∠ACB=90°,∠CAD=30°,AC=BC,
∴∠CAB=∠ABC=45°
∴∠BAD=∠BAC﹣∠CAD=45﹣30=15°,
∵△ACD≌△BCE,
∴∠CBE=30°,
∴∠ABF=45+30=75°,
∴∠AFB=180﹣15﹣75=90°,
∴AD⊥BE.
④证明:如图,
过D作DM⊥AC于M,过D作DN⊥BC于N.
∵∠CAD=30°,且DM=![]() AC,
AC,
∵AC=AD,∠CAD=30°,∴∠ACD=75°,
∴∠NCD=90°﹣∠ACD=15°,∠MDC=∠DMC﹣∠ACD=15°,
在△CMD和△CND中,
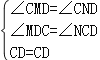 ,
,
∴△CMD≌△CND,
∴CN=DM=![]() AC=
AC=![]() BC,
BC,
∴CN=BN.
∵DN⊥BC,
∴BD=CD.∴④正确.
所以4个结论都正确.
故选D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
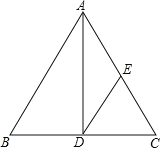
【题目】如图,AD是等腰三角形ABC的底边BC上的高,DE∥AB,交AC于点E,试找出图中的一个等腰三角形(△ABC除外),并说明理由.我找的等腰三角形是 理由:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适合用普查方式的是( )
A.了解2016年最新一批炮弹的杀伤半径
B.了解阳泉电视台《XX》栏目的收视率
C.了解黄河的鱼的种类
D.了解某班学生对“山西精神”的知晓率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.了解某班同学的身高情况适合用全面调查
B.数据4、5、5、6、0的平均数是5
C.数据2、3、4、2、3的中位数是4
D.甲、乙两组数据的平均数相同,方差分别是S甲2=3.2,S乙2=2.9,则甲组数据更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.

①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com