
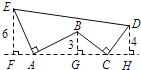
【题目】如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是 .

【答案】50.
【解析】
试题分析:由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≌△ABG,所以AF=BG,AG=EF;同理证得△BGC≌△DHC,GC=DH,CH=BG,故FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH∠FED=∠EFA=∠BGA=90°,
∠EAF+∠BAG=90°,∠ABG+∠BAG=90°∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG△EFA≌△ABG
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16
故S=![]() (6+4)×16﹣3×4﹣6×3=50.
(6+4)×16﹣3×4﹣6×3=50.
故答案为50.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
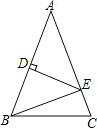
【题目】如图:△ABC中,∠ACB=90°,∠CAD=30°,AC=BC=AD,CE⊥CD,且CE=CD,连接BD,DE,BE,则下列结论:①∠ECA=165°,②BE=BC;③AD⊥BE;④![]() =1.其中正确的是( )
=1.其中正确的是( )

A.①②③ B.①②④ C.①③④ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于同一平面内的三条直线a,b,c,给出下列5个判断:①a∥b②b∥c;③a⊥b;④a∥c;⑤a⊥c.请以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题(至少写两个命题).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
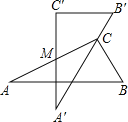
【题目】如图是两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=5,则这块直角三角板顶点A、A′之间的距离等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
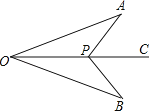
【题目】如图,点P是∠AOB的角平分线OC上一点,分别连接AP、BP,若再添加一个条件即可判定△AOP≌△BPO,则一下条件中:①∠A=∠B;②∠APO=∠BPO;③∠APC=∠BPC; ④AP=BP;⑤OA=OB.其中一定正确的是 (只需填序号即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com