
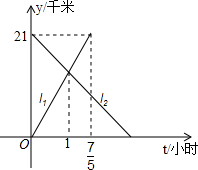
 甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系
甲乙两人分别从相距21千米的A,B两地同时出发,相向而行,如图,l1,l2分别表示甲乙两人距A地的距离y(千米)与时间t(小时)之间的关系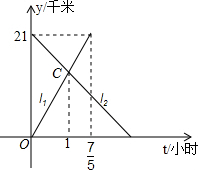 解:(1)由图象可得:l1=kt,
解:(1)由图象可得:l1=kt,| 7 |
| 5 |
| 7 |
| 5 |
|
|
| 7 |
| 2 |
| 7 |
| 2 |
| 7 |
| 5 |


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
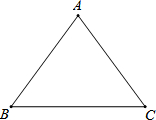 如图,在△ABC中,AB=AC,BC=32,tanC=
如图,在△ABC中,AB=AC,BC=32,tanC=| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知抛物线y=
如图,已知抛物线y=| 1 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
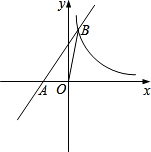 如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,0),与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A(-1,0),与反比例函数y=| m |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| a |
| c |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
 在⊙O中,AB为⊙0的直径,AC是弦,OC=4cm∠OAC=60°,如图所示,一动点M从点A出发,在⊙O上按逆时针方向运动,当S=△MAO=S△AOC时,动点M所经过的弧长是
在⊙O中,AB为⊙0的直径,AC是弦,OC=4cm∠OAC=60°,如图所示,一动点M从点A出发,在⊙O上按逆时针方向运动,当S=△MAO=S△AOC时,动点M所经过的弧长是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com