
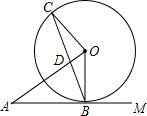
 如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA 交⊙O于点C,连结BC,交DA于点D.
如图,⊙O与射线AM相切于点B,⊙O的半径为3.连结DA,作OC⊥OA 交⊙O于点C,连结BC,交DA于点D.分析 (1)首先根据OA⊥OC得到∠C+∠ODC=90°,然后根据AM是⊙O的切线得到∠CBO+∠ABD=90°,进一步得到∠ABD=∠ADB,利用等角对等边得到AB=AD;
(2)首先根据cos∠A=$\frac{4}{5}$得到tan∠A=$\frac{3}{4}$,然后在Rt△AOB中,OB=3得到OA=5,AB=4,从而求得OD的长;
(3)假设△AOB与△DCO全等,根据CD不可能与OB平行,得到∠CDO不可能与∠AOB对应相等,得到∠A=60°后根据OB=3,求得AB=$\sqrt{3}$.
解答 (1)证明:∵OA⊥OC,
∴∠C+∠ODC=90°,
∵AM是⊙O的切线,
∴OB⊥AM,
即∠CBO+∠ABD=90°,
∵OC=OB,
∴∠C=∠OBC,
∴∠ABD=∠ADB,
即AB=AD;
(2)解:∵cos∠A=$\frac{4}{5}$,
∴tan∠A=$\frac{3}{4}$,
在Rt△AOB中,OB=3,
∴OA=5,AB=4,
∴OD=OA-AD=OA-AB=1;
(3)解:假设△AOB与△DCO全等,
∵CD不可能与OB平行,
∴∠CDO不可能与∠AOB对应相等,
∴∠CDO=∠A,
∵∠ABD=∠ADB=∠CDO,
∴∠A=60°,
∵OB=3,
∴AB=$\sqrt{3}$.
点评 本题考查了圆的综合知识及锐角三角函数、存在性问题,对于存在性问题,常常首先假设存在,然后从存在出发,如果能够得到结论就存在,否则就不存在,综合性较强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
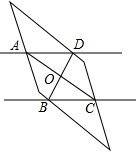 如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.
如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
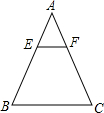 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{3}$,S四边形BCFE=15,则S△ABC=16.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.
如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
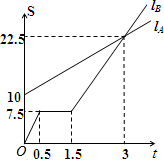 如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:
如图,LA,LB分别表示A步行与B骑车在同一路上行驶的路程S(千米)与时间t(小时)的关系.根据图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )
如图,AD∥BC,∠ABC的平分线BP与∠BAD的平分线AP相交于点P,作PE⊥AB于点E,若PE=2,则两平行线AD与BC间的距离为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com