
【题目】如图,在平行四边形![]() 中,以
中,以![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 于点
于点![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接AG并延长交
,连接AG并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,则下列结论:①四边形
,则下列结论:①四边形![]() 是菱形;②
是菱形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确的有( )
.正确的有( )

A.①③④B.①③⑤C.②③④⑤D.①②③④⑤
【答案】A
【解析】
①根据尺规作图得到直线AE是∠FAB的角平分线,也是线段BF的垂直平分线,根据线段垂直平分线的性质、菱形的判定定理即可判断;②根据菱形的性质,在Rt△ABO中,利用勾股定理可求得AE的长,即可判断;③利用菱形的面积公式“对角线乘积的一半”可求得![]() ,即可判断;④根据
,即可判断;④根据![]() ,可求得
,可求得![]() 的长,即可判断;⑤在Rt△AHE中,根据直角三角形的性质可求得HO的长,即可判断.
的长,即可判断;⑤在Rt△AHE中,根据直角三角形的性质可求得HO的长,即可判断.
①由尺规作图的过程可知,直线AE是∠FAB的角平分线,也是线段BF的垂直平分线,
∴AF=AB,EF=EB,∠FAE=∠BAE,
∵AD∥BC,
∴∠FAE=∠AEB,
∴∠AEB=∠BAE,
∴BA=BE,
∴BA=BE=AF=FE,
∴四边形ABEF是菱形,故①正确;
②∵四边形ABEF是菱形,
∴AE⊥BF,AO=OE,BO=OF=3,
在Rt△ABO中,AB=4,BO =3,∠AOB=90![]() ,
,
∴![]() ,
,
∴AE=2AO=![]() ,故②错误;
,故②错误;
③∵四边形ABEF是菱形,
∴![]() ,故③正确;
,故③正确;
④∵四边形ABEF是菱形,
∴BE=AB=4,
∵![]() ,
,
∴![]() ,故④正确;
,故④正确;
⑤∵四边形ABEF是菱形,
∴O是E的中点,
∴在Rt△AHE中,HO是斜边AE的中线,
∴HO![]() ,故⑤错误;
,故⑤错误;
综上,①③④正确,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个
”中的每个![]() 内,填入
内,填入![]() ,
,![]() ,
,![]() ,
,![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若![]() ,请推算
,请推算![]() 内的符号;
内的符号;
(3)在“![]() ”的内填入符号后,使计算所得数最小,直接写出这个最小数.
”的内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
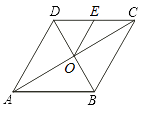
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
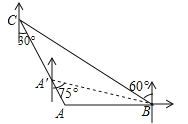
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ABC为等边三角形,以AB边为腰作等腰Rt
ABC为等边三角形,以AB边为腰作等腰Rt![]() ABD,∠BAD=90
ABD,∠BAD=90![]() ,AC与BD交于点E,连接CD,过点D作DF⊥BC交BC延长线于点F.
,AC与BD交于点E,连接CD,过点D作DF⊥BC交BC延长线于点F.
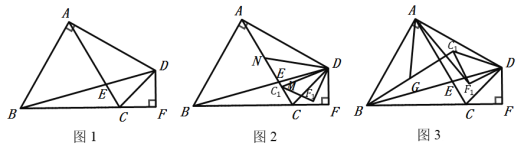
(1)如图1,若DF=1,AB= ;AE= ;
(2)如图2,将![]() CDF绕点D顺时针旋转至△C1DF1的位置,点C,F的对应点分别为C1,F1,当DC1平分∠EDC时,DC1与AC交于点M,在AM上取点N,使AN=DM,连接DN,求tan∠NDM的值.
CDF绕点D顺时针旋转至△C1DF1的位置,点C,F的对应点分别为C1,F1,当DC1平分∠EDC时,DC1与AC交于点M,在AM上取点N,使AN=DM,连接DN,求tan∠NDM的值.
(3)如图3,将![]() CDF绕点D顺时针旋转至
CDF绕点D顺时针旋转至![]() C1DF1的位置,点C,F的对应点分别为C1,F1,连接AF1、BC1,点G是BC1的中点,连接AG.求
C1DF1的位置,点C,F的对应点分别为C1,F1,连接AF1、BC1,点G是BC1的中点,连接AG.求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】越野自行车是中学生喜爱的交通工具,市场巨大,竟争也激烈.某品牌经销商经营的![]() 型车去年销售总额为
型车去年销售总额为![]() 万元,今年每辆售价比去年降低
万元,今年每辆售价比去年降低![]() 元,若卖出的数量相同,销售总额将比去年减少
元,若卖出的数量相同,销售总额将比去年减少![]() .
.
(1)设今年![]() 型车每辆销售价为
型车每辆销售价为![]() 元,求
元,求![]() 的值;
的值;
(2)该品牌经销商计划新进一批![]() 型车和新款
型车和新款![]() 型车共
型车共![]() 辆,且
辆,且![]() 型车的进货数量不超过
型车的进货数量不超过![]() 型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批售出后获利最多?
型车数量的两倍,请问应如何安排两种型号车的进货数量,才能使这批售出后获利最多?
![]() 、
、![]() 两种型号车今年的进货和销售价格表
两种型号车今年的进货和销售价格表
|
| |
进货价 |
|
|
销售价 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴正半轴交于点
轴正半轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与该抛物线交于
与该抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 位于点
位于点![]() 左侧),与抛物线对称轴交于点
左侧),与抛物线对称轴交于点![]() .
.
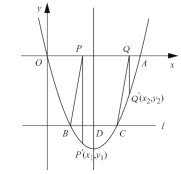
(1)求![]() 的值;
的值;
(2)设![]() 、
、![]() 是
是![]() 轴上的点(点
轴上的点(点![]() 位于点
位于点![]() 左侧),四边形
左侧),四边形![]() 为平行四边形.过点
为平行四边形.过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,与抛物线交于点
轴的垂线,与抛物线交于点![]() 、
、![]() .若
.若![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点为D的抛物线y=﹣x2+bx+c交x轴于A、B(3,0),交y轴于点C,直线y=﹣![]() x+m经过点C,交x轴于E(4,0).
x+m经过点C,交x轴于E(4,0).
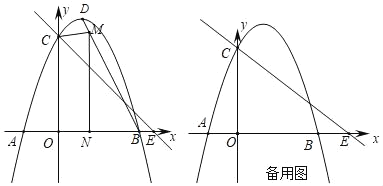
(1)求出抛物线的解析式;
(2)如图1,点M为线段BD上不与B、D重合的一个动点,过点M作x轴的垂线,垂足为N,设点M的横坐标为x,四边形OCMN的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点P为x轴的正半轴上一个动点,过P作x轴的垂线,交直线y=﹣![]() x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
x+m于G,交抛物线于H,连接CH,将△CGH沿CH翻折,若点G的对应点F恰好落在y轴上时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() ,点D落在线段AB上,连接BE.
,点D落在线段AB上,连接BE.

(1)求证:DC平分![]() ;
;
(2)试判断BE与AB的位置关系,并说明理由:
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com