
【题目】如图,![]() 中,
中,![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() ,点D落在线段AB上,连接BE.
,点D落在线段AB上,连接BE.

(1)求证:DC平分![]() ;
;
(2)试判断BE与AB的位置关系,并说明理由:
(3)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)BE⊥AB,理由见解析;(3)![]() .
.
【解析】
(1)根据旋转的性质可得AC=CD,∠A=∠CDE,再由等腰三角形的性质得到∠A=∠ADC即可证明∠ADC=∠CDE;
(2)根据旋转的性质得到∠ACD=∠BCE,CB=CE,AC=CD,从而得出∠CAD=∠ADC=∠CBE=∠CEB,再根据∠ACB=90°即可得到∠ABE=90°;
(3)设BD=BE=a,根据勾股定理计算出AB=DE=![]() ,表达出AD,再证明△ACD∽△BCE,得到
,表达出AD,再证明△ACD∽△BCE,得到![]() 即可.
即可.
解:(1)由旋转可知:AC=CD,∠A=∠CDE,
∴∠A=∠ADC,
∴∠ADC=∠CDE,即DC平分∠ADE;
(2)BE⊥AB,
理由:由旋转可知,∠ACD=∠BCE,CB=CE,AC=CD,
∴∠CAD=∠ADC=∠CBE=∠CEB,
又∵∠ACB=90°,
∴∠CAD+∠ABC=90°,
∴∠CBE+∠ABC=90°,
即∠ABE=90°,
∴BE⊥AB;
(3)∵∠ABE=90°,BD=BE,
∴设BD=BE=a,则![]() ,
,
又∵AB=DE,
∴AB=![]() ,则AD=
,则AD=![]() ,
,
由(2)可知,∠ACD=∠BCE,∠CAD=∠ADC=∠CBE=∠CEB,
∴△ACD∽△BCE,
∴![]() ,
,
∴tan∠ABC=![]() .
.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,以
中,以![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 于点
于点![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接AG并延长交
,连接AG并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,则下列结论:①四边形
,则下列结论:①四边形![]() 是菱形;②
是菱形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确的有( )
.正确的有( )

A.①③④B.①③⑤C.②③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+8于A,B两点,若反比例函数y=![]() (x>0)的图象与△ABC有公共点,则k的取值范围是_____.
(x>0)的图象与△ABC有公共点,则k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=4,边BC在其所在的直线上平移,平移后得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
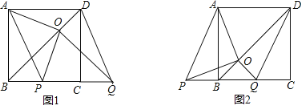
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并利用图1加以证明.
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤4),求y与x之间的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到加工粮食任务,要求![]() 天加工完
天加工完![]() 吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量
吨粮食.该企业安排甲、乙两车间共同完成加工任务.乙车间因维修设备,中途停工一段时间,维修设备后提高了加工效率,继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工粮食数量![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图①所示;未加工粮食
(天)之间的函数关系如图①所示;未加工粮食![]() (吨)与甲车间加工时间
(吨)与甲车间加工时间![]() (天)之间的函数关系如图②所示、请结合图象解答下列问题:
(天)之间的函数关系如图②所示、请结合图象解答下列问题: ![]()
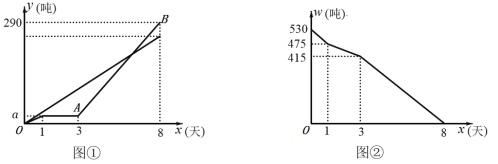
(1)甲车间每天加工粮食 吨,![]() ;
;
(2)求乙车间维修设备后,乙车间加工粮食数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求加工![]() 吨粮食需要几天完成.
吨粮食需要几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C是半径为2的⊙O上三个点,AB为直径,∠BAC的平分线交圆于点D,过点D作AC的垂线交AC得延长线于点E,延长线ED交AB得延长线于点F.
(1)判断直线EF与⊙O的位置关系,并证明.
(2)若DF=![]() ,求tan∠EAD的值.
,求tan∠EAD的值.
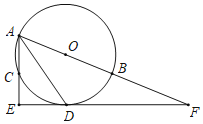
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC中AB边上一点,以点O为圆心,OA的长为半径作⊙O,⊙O恰好经过点C,且与边BC,AB分别交于E,F两点.连接AE,过点E作⊙O的切线,交线段BF于点M,交AC的延长线于点N,且EM=BM,EB=AO.
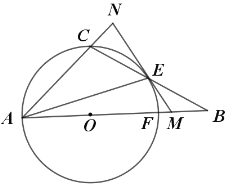
(1)求![]() 的度数;
的度数;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昌云中学计划为地理兴趣小组购买大、小两种地球仪,若购买1个大地球仪和3个小地球仪需要136元;若购买2个大地球仪和1个小地球仪需要132元.
(1)求每个大地球仪和每个小地球仪各多少元;
(2)昌云中学决定购买以上两种地球仪共30个,总费用不超过960元,那么昌云中学最多可以购买多少个大地球仪.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com