
【题目】![]() ABC为等边三角形,以AB边为腰作等腰Rt
ABC为等边三角形,以AB边为腰作等腰Rt![]() ABD,∠BAD=90
ABD,∠BAD=90![]() ,AC与BD交于点E,连接CD,过点D作DF⊥BC交BC延长线于点F.
,AC与BD交于点E,连接CD,过点D作DF⊥BC交BC延长线于点F.
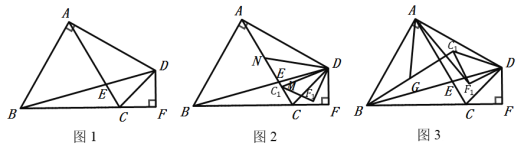
(1)如图1,若DF=1,AB= ;AE= ;
(2)如图2,将![]() CDF绕点D顺时针旋转至△C1DF1的位置,点C,F的对应点分别为C1,F1,当DC1平分∠EDC时,DC1与AC交于点M,在AM上取点N,使AN=DM,连接DN,求tan∠NDM的值.
CDF绕点D顺时针旋转至△C1DF1的位置,点C,F的对应点分别为C1,F1,当DC1平分∠EDC时,DC1与AC交于点M,在AM上取点N,使AN=DM,连接DN,求tan∠NDM的值.
(3)如图3,将![]() CDF绕点D顺时针旋转至
CDF绕点D顺时针旋转至![]() C1DF1的位置,点C,F的对应点分别为C1,F1,连接AF1、BC1,点G是BC1的中点,连接AG.求
C1DF1的位置,点C,F的对应点分别为C1,F1,连接AF1、BC1,点G是BC1的中点,连接AG.求![]() 的值;
的值;
【答案】(1)AB=![]() ,AE=2;(2)tan∠NDM=
,AE=2;(2)tan∠NDM=![]() ;(3)
;(3)![]() =
=![]()
【解析】
(1)作AM⊥BC于M,AN⊥DF于N,EH⊥AB于H,在BF上取一点K,使得BK=DK,先证明四边形AMFN是正方形,然后可推出Rt△ACM≌Rt△AND,可得CM=DN,CF=DF=1,根据∠ABC=60°,得出∠ABD=45°,∠KBD=∠KDB=15°,∠DKF=∠KBD+∠KDB=30°,可得出KD=KB=2,KF=![]() ,即可推出BF=2+
,即可推出BF=2+![]() ,BC=AB=
,BC=AB=![]() +1,设AE=x,则AH=
+1,设AE=x,则AH=![]() x,BH=HE=
x,BH=HE=![]() x,即可求出AE;
x,即可求出AE;
(2)先证明∠DEC=∠DCE=75°,然后根据等腰三角形的性质得出DM⊥AM,推出∠AMD=90°,∠ADM=60°,设DM=AN=a,可得AM=![]() a,NM=(
a,NM=(![]() 1)a,即可得出答案;
1)a,即可得出答案;
(3)延长FG到M,延长BA交F1C1的延长线于N,使得GM=F1G,则△GMB≌△GF1C1,可推出∠MBA=∠N,然后证明△ABM≌△ADF1,可推出△AMF1是等腰直角三角形,AG⊥MF1,AG=GF1,即可证明结论.
(1)如图1中,作AM⊥BC于M,AN⊥DF于N,EH⊥AB于H,在BF上取一点K,使得BK=DK,
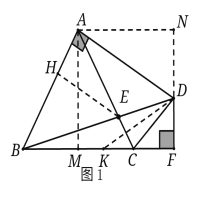
∵∠BAD=∠BFD=90°,
∴∠BAD+∠BFD=180°,
∴∠ABF+∠ADF=180°,
∵∠ABC=60°,
∴∠ADF=120°,
∴∠ADN=60°,
∴△AMB≌△AND(AAS),
∴AM=AN,
∵四边形AMFN是矩形,
∴四边形AMFN是正方形,
∴FM=FN,
∴Rt△ACM≌Rt△AND,
∴CM=DN,
∴CF=DF=1,
∵∠ABC=60°,
∴∠ABD=45°,
∴∠KBD=∠KDB=15°,
∴∠DKF=∠KBD+∠KDB=30°,
∴KD=KB=2,KF=![]() ,
,
∴BF=2+![]() ,BC=AB=
,BC=AB=![]() +1,
+1,
设AE=x,则AH=![]() x,BH=HE=
x,BH=HE=![]() x,
x,
∴![]() x+
x+![]() x=
x=![]() +1,
+1,
解得x=2,
∴AE=2,
故答案为:AB=![]() +1,AE=2;
+1,AE=2;
(2)∵∠BAD=90°,∠BAC=60°,
∴∠CAD=90°60°=30°,
∵△ABC为等边三角形,△ABD为等腰直角三角形,
∴∠EAD=30°,∠ADB=45°,∠ACB=60°,
∴∠DEC=75°,
由(1)可得CF=DF,
∴∠DCF=45°,
∴∠DCE=180°-∠ACB-∠DCF=75°,
∵∠DEC=∠DCE=75°,
∴DE=DC,
∵DC1平分∠EDC,
∴DM⊥AM,
∴∠AMD=90°,∠ADM=60°,
设DM=AN=a,易知AM=![]() a,NM=(
a,NM=(![]() 1)a,
1)a,
∴tan∠NDM=![]() =
=![]() ;
;
(3)如图3,延长FG到M,延长BA交F1C1的延长线于N,使得GM=F1G,则△GMB≌△GF1C1,
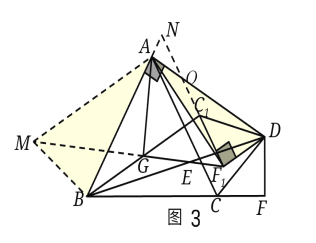
∴BM=F1C1=DF1,∠BMG=∠GF1N,
∴BM//F1N,
∴∠MBA=∠N,
∵∠NAO=∠OF1D=90°,∠AON=∠DOF1,
∴∠N=∠ADF1,
∴∠ABM=∠ADF1,
∵AB=AD,
∴△ABM≌△ADF1,
∴AM=AF1,∠MAB=∠DAF1,
∴∠MAF1=∠BAD=90°,
∴△AMF1是等腰直角三角形,
∴AG⊥MF1,AG=GF1,
∴AF1=![]() AG,即
AG,即![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:点![]() 为
为![]() 边上的一个动点.
边上的一个动点.
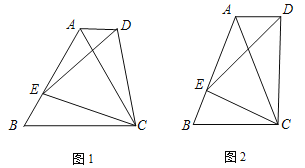
(1)如图1,若![]() 是等边三角形,以
是等边三角形,以![]() 为边在
为边在![]() 的同侧作等边
的同侧作等边![]() ,连接
,连接![]() .试比较
.试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(2)如图2,若![]() 中,
中,![]() ,以
,以![]() 为底边在
为底边在![]() 的同侧作等腰
的同侧作等腰![]() ,且
,且![]() ∽
∽![]() ,连接
,连接![]() .试判断
.试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
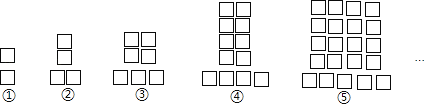
【题目】如图图形都是由同样大小的正方形“□”按照一定规律排列的,其中图①中共有2个正方形,图②中共有4个正方形,图③中共有7个正方形,图④中共有12个正方形,图⑤中共有21个正方形,……,照此规律排列下去,则图⑩中正方形的个数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).

(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,以
中,以![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 于点
于点![]() ,分别以点
,分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连接AG并延长交
,连接AG并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,则下列结论:①四边形
,则下列结论:①四边形![]() 是菱形;②
是菱形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .正确的有( )
.正确的有( )

A.①③④B.①③⑤C.②③④⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
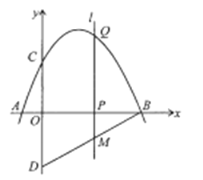
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是线段
是线段![]() 上的一个动点.设点
上的一个动点.设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)连接![]() ,
,![]() ,当点
,当点![]() 运动到何处时,
运动到何处时,![]() 面积最大?最大面积是多少?并求出此时点
面积最大?最大面积是多少?并求出此时点![]() 的坐标;
的坐标;
(3)在第![]() 问的前提下,在
问的前提下,在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 值最小,求出
值最小,求出![]() 的最小值并直接写出此时点
的最小值并直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
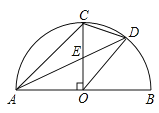
【题目】如图,AB是半圆O的直径,半径OC⊥AB于点O,点D是![]() 的中点,连接CD、OD.下列四个结论:①AC
的中点,连接CD、OD.下列四个结论:①AC![]() OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
OD;②CE=OE;③△ODE∽△ADO;④∠ADC=∠BOD.其中正确结论的序号是( )
A.①④B.①②④C.②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com