
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 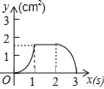 C.
C.  D.
D. 
【答案】C
【解析】试题分析:首先根据正方形的边长与动点P、Q的速度可知动点Q始终在AB边上,而动点P可以在BC边、CD边、AD边上,再分三种情况进行讨论:①0≤x≤1;②1<x≤2;③2<x≤3;分别求出y关于x的函数解析式,然后根据函数的图象与性质即可求解.
解:由题意可得BQ=x.
①0x1时,P点在BC边上,BP=3x,
则△BPQ的面积=![]() BPBQ,
BPBQ,
解y=![]() 3xx=
3xx=![]() x2;故B选项错误;
x2;故B选项错误;
②1<x2时,P点在CD边上,
则△BPQ的面积=![]() BQBC,
BQBC,
解y=![]() x3=
x3=![]() x;故D选项错误;
x;故D选项错误;
③2<x3时,P点在AD边上,AP=93x,
则△BPQ的面积=![]() APBQ,
APBQ,
解y=![]() (93x)x=
(93x)x=![]() x
x![]() x2;故C选项错误.
x2;故C选项错误.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() 的顶点坐标为:
的顶点坐标为:![]() ,
,![]() ,
,![]() .
.

(1)将![]() 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得![]() .画出
.画出![]() 并写出
并写出![]() 的顶点坐标;
的顶点坐标;
(2)请判断![]() 的形状并求它的面积.
的形状并求它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是从一副扑克牌中取出的两组牌,分别是黑桃1,2,3,4和方块1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树状图)加以分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
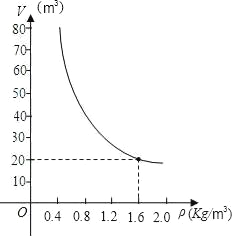
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题(1)、(2)、(3).
例:解绝对值方程:![]() .
.
解:讨论:①当![]() ≥0时,原方程可化为
≥0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
②当![]() <0时,原方程可化为
<0时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
∴原方程的解为![]() 和
和![]() .
.
问题(1):依例题的解法,方程![]() 的解是 ;
的解是 ;
问题(2):尝试解绝对值方程:![]() ;
;
问题(3):在理解绝对值方程解法的基础上,解方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】指出下列问题中的总体、个体、样本:
(1)为了估计某块玉米试验田里的单株平均产量,从中抽取![]() 株进行实测;
株进行实测;
(2)某学校为了了解学生完成课外作业的时间,从中抽样调查了![]() 名学生完成课外作业的时间进行分析.
名学生完成课外作业的时间进行分析.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com