
 如图,效果家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6cm,他想知道剩余阴影部分的面积,你能帮助小刚利用所学过的因式分解计算吗?请写出利用因式分解的求解的过程(π取3)
如图,效果家门口的商店在装修,他发现工人正在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6cm,他想知道剩余阴影部分的面积,你能帮助小刚利用所学过的因式分解计算吗?请写出利用因式分解的求解的过程(π取3) 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
| A、3.5,3 | B、3,4 |
| C、3,3.5 | D、4,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
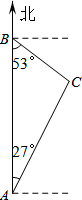 如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.| 9 |
| 20 |
| 9 |
| 10 |
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com