
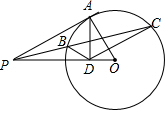
 如图,PBC为⊙O的割线,AD⊥OP于点D,且∠APD=∠OAD
如图,PBC为⊙O的割线,AD⊥OP于点D,且∠APD=∠OAD分析 (1)利用直角三角形的两锐角互余以及等量代换证得∠OAP=90°,利用切线的判定定理证得;
(2)连接OA、OC,如图,根据切线的性质得∠OAP=90°,由AD⊥OP得到∠ADP=∠ADO=90°,再根据相似三角形的判定易得Rt△PAD∽Rt△POA,则PA2=PD•PO,同理可得Rt△OAD∽Rt△OPA,则OA2=OD•OP;Rt△PAD∽Rt△AOD,则AD2=PD•DO,由于OA2=OD•OP,OC=OA,得到OC2=OD•OP,加上∠POC=∠COD,则根据相似三角形的判定方法得到△POC∽△COD;然后根据切割线定理得PA2=PB•PC,则PB•PC=PD•PO,加上∠BPD=∠OPC,于是可判断△PBD∽△POC,
所以△PBD∽△COD,利用相似比得到∠BDP=∠ODC,
(3)利用△PBD∽△COD证得PD•OD=BD•CD,由此得到AD2=BD•CD.
解答 证明:(1)∵AD⊥OP,
∴△APD是直角三角形,
∴∠APD+∠PAD=90°,
又∵∠APD=∠OAD,
∴∠PAD+∠OAD=90°,即∠OAP=90°,
∴PA⊥OA,
∴PA是切线;
(2)解:连接OA、OC,如图,
∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵AD⊥OP,
∴∠ADP=∠ADO=90°,
∵∠APO=∠DPA,
∴Rt△PAD∽Rt△POA,
∴PA:PO=PD:PA,即PA2=PD•PO,
同理可得Rt△OAD∽Rt△OPA,则OA2=OD•OP,
Rt△PAD∽Rt△AOD,则AD2=PD•DO,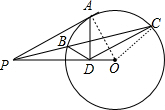
∵OA2=OD•OP,OC=OA,
∴OC2=OD•OP,即OC:OD=OP:OC,
而∠POC=∠COD,
∴△POC∽△COD;
∵PA为⊙O的切线,PBC为⊙O的割线,
∴PA2=PB•PC,
∴PB•PC=PD•PO,即PB:PO=PD:PC,
而∠BPD=∠OPC,
∴△PBD∽△POC,
∴△PBD∽△COD,
∴∠BDP=∠ODC;
(3)解:∵△PBD∽△COD,
∴PD:CD=BD:OD,即PD•OD=BD•CD,
∴AD2=BD•CD.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了相似三角形的判定与性质、切割线定理.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
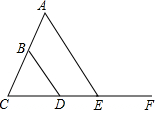 如图,在△BCD中,BC=4,BD=5,
如图,在△BCD中,BC=4,BD=5,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5.86% | B. | 5.88% | C. | 5.84% | D. | 5.82% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
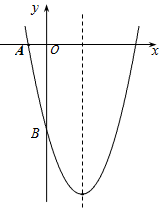 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com