
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
【答案】证明:(1)见解析
(2)见解析
【解析】
证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∴∠ABF=∠ECF.
∵EC=DC,∴AB=EC.
在△ABF和△ECF中,∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,
∴△ABF≌△ECF.
(2)证法一:由(1)知AB=EC,又AB∥EC,∴四边形ABEC是平行四边形.∴AF=EF,BF=CF.
∵四边形ABCD是平行四边形,∴∠ABC=∠D,又∵∠AFC=2∠D,∴∠AFC=2∠ABC.
∵∠AFC=∠ABF+∠BAF,∴∠ABF=∠BAF.∴FA=FB.
∴FA=FE=FB=FC,∴AE=BC.∴□ABEC是矩形.
证法二:由(1)知AB=EC,又AB∥EC,∴四边形ABEC是平行四边形.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠D=∠BCE.
又∵∠AFC=2∠D,∴∠AFC=2∠BCE.
∵∠AFC=∠FCE+∠FEC,∴∠FCE=∠FEC.∴∠D=∠FEC.
∴AE=AD.
又∵CE=DC,∴AC⊥DE,即∠ACE=90°.
∴□ABEC是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
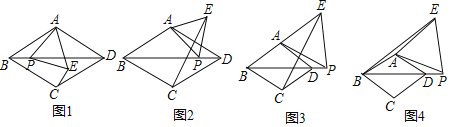
【题目】在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随点P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是_________,CE与AD的位置关系是____________________;
(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理).
(3)如图4,当点P在线段BD的延长线上时,连接BE,若![]() ,求四边形ADPE的面积.
,求四边形ADPE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为
是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,因为![]() ,所以可用、
,所以可用、![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是__________,小数部分是__________.
的整数部分是__________,小数部分是__________.
(2)如果![]() 的整数部分为
的整数部分为![]() ,小数部分为
,小数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知![]() ,其中
,其中![]() 是整数,且
是整数,且![]() .则求
.则求![]() 的平方根的值.
的平方根的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到商场购买某个牌子的铅笔![]() 支,用了
支,用了![]() 元(
元(![]() 为整数).后来他又去商场时,发现这种牌子的铅笔降阶
为整数).后来他又去商场时,发现这种牌子的铅笔降阶![]() ,于是他比上一次多买了
,于是他比上一次多买了![]() 支铅笔,用了
支铅笔,用了![]() 元钱,那么小明两次共买了铅笔________支.
元钱,那么小明两次共买了铅笔________支.
查看答案和解析>>
科目:初中数学 来源: 题型:
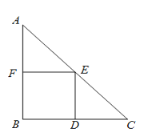
【题目】如图,在Rt△ABC中,∠B=90°,AB=BC,AC=![]() .四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积为( )
.四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的面积为( )
A.25.B.![]() .C.5.D.10.
.C.5.D.10.
查看答案和解析>>
科目:初中数学 来源: 题型:
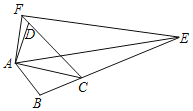
【题目】如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,∠EAF=![]() ∠BAD,若DF=1,BE=5,则线段EF的长为( )
∠BAD,若DF=1,BE=5,则线段EF的长为( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 | 6 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折合成综合成绩(综合成绩的满分仍为100分).
(1)这6名选手笔试成绩的中位数是________分,众数是________分;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
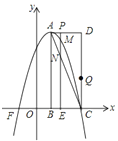
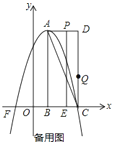
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 过点
过点![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 于点
于点![]() .
.
![]() 直接写出点
直接写出点![]() 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积最大?最大值为多少?
的面积最大?最大值为多少?
![]() 点
点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 运动,当
运动,当![]() 为何值时,在线段
为何值时,在线段![]() 上存在点
上存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?
为顶点的四边形为菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
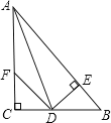
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com