
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点的抛物线
为顶点的抛物线![]() 过点
过点![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 运动,运动时间为
运动,运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 于点
于点![]() .
.
![]() 直接写出点
直接写出点![]() 的坐标,并求出抛物线的解析式;
的坐标,并求出抛物线的解析式;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积最大?最大值为多少?
的面积最大?最大值为多少?
![]() 点
点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向点
向点![]() 运动,当
运动,当![]() 为何值时,在线段
为何值时,在线段![]() 上存在点
上存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?
为顶点的四边形为菱形?
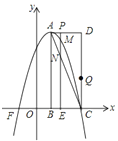
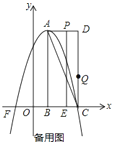
【答案】![]() ;
;![]()
![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,
为顶点的四边形为菱形时,![]() 或
或![]() .
.
【解析】
(1)A点的横坐标同B点,纵坐标同D点,然后设顶点式求解抛物线即可;
(2)求解直线![]() 的解析式为
的解析式为![]() ,设
,设![]() 从而表示出M和N的坐标;将
从而表示出M和N的坐标;将![]() 的面积拆分为
的面积拆分为![]() 和
和![]() 两部分进行计算即可;
两部分进行计算即可;
(3)本问题分![]() 在
在![]() 上方和下方两种情况讨论,利用四边形
上方和下方两种情况讨论,利用四边形![]() 是菱形的四边相等条件,将相关线段用t表示;当
是菱形的四边相等条件,将相关线段用t表示;当![]() 在
在![]() 上方时,运用三角形相似进行求解,当
上方时,运用三角形相似进行求解,当![]() 在
在![]() 下方时,运用勾股定理进行求解.
下方时,运用勾股定理进行求解.
![]() ,
,
由题意知,可设抛物线解析式为![]()
∵抛物线过点![]() ,
,
∴![]() ,
,
解得![]() .
.
∴抛物线的解析式为![]() ,即
,即![]() ;
;
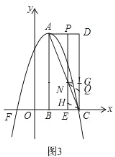
![]() 如图
如图![]() ,
,
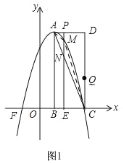
∵![]() ,
,![]() ,
,
∴可求直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() .
.
∴将![]() 代入
代入![]() 中,解得点
中,解得点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴把![]() ,代入抛物线的解析式中,可求点
,代入抛物线的解析式中,可求点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
又点![]() 到
到![]() 的距离为
的距离为![]() ,
,![]() 到
到![]() 的距离为
的距离为![]() ,
,
即![]()
![]() .
.
当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
![]() 由题意和
由题意和![]() 知,
知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,可求
,可求![]() ,
,
当![]() 在
在![]() 上方时,如图
上方时,如图![]() ,过点
,过点![]() 作
作![]() ,
,
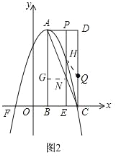
由四边形![]() 是菱形,可知:
是菱形,可知:![]() ,
,
此时,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
解得:![]() ,
,
当点![]() 在
在![]() 下方时,如图
下方时,如图![]() ,
,
由四边形![]() 是菱形,可知:
是菱形,可知:![]() ,
,
∴![]() ,
,![]() ,
,
在直角三角形![]() 中,
中,![]() ,
,
∴![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,
为顶点的四边形为菱形时,![]() 或
或![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=―![]() x2+(6―
x2+(6―![]() )x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
)x+m―3与x轴交于A(x1,0)、B(x2,0)两点(x1<x2),交y轴于C点,且x1+x2=0。
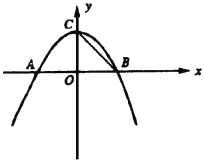
(1)求抛物线的解析式,并写出顶点坐标及对称轴方程。
(2)在抛物线上是否存在一点P使△PBC≌△OBC,若存在,求出点P的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EA⊥AB,BC⊥AB,AB=AE=2BC,D为AB中点,在“①DE=AC;②DE⊥AC;③∠EAF=∠ADE;④∠CAB=30°”这四个结论中,正确的个数有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像与正比例函数
的图像与正比例函数![]() 的图像都经过点
的图像都经过点![]() ,点
,点![]() 在反比例函数
在反比例函数![]() 的图像上,点
的图像上,点![]() 在正比例函数
在正比例函数![]() 的图像上.
的图像上.
(1)求此正比例函数的解析式;
(2)求线段AB的长;
(3)求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一棵树CD的10m高处的B点有两只猴子,它们都要到A处池塘边喝水,其中一只猴子沿树爬下走到离树20m处的池塘A处,另一只猴子爬到树顶D后直线跃入池塘的A处.如果两只猴子所经过的路程相等,试问这棵树多高?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.
根据图象进行以下探究:
⑴请问甲乙两地的路程为 ;
⑵求慢车和快车的速度;
⑶求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围;
⑷如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km),请在右图中画出y1、y2与x的函数图像.


查看答案和解析>>
科目:初中数学 来源: 题型:
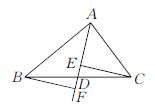
【题目】如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E,F,连结CE,BF.添加一个条件,使得△BDF≌△CDE,你添加的条件是_____________________(不添加辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
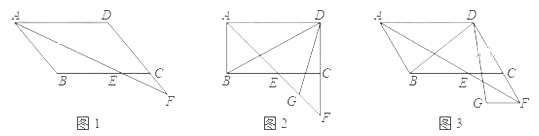
【题目】在平行四边形ABCD中,E是BC上任意一点,延长AE交DC的延长线与点F.
(1)在图中当CE=CF时,求证:AF是∠BAD的平分线.
(2)在(1)的条件下,若∠ABC=90°,G是EF的中点(如图),请求出∠BDG的度数.
(3)如图,在(1)的条件下,若∠BAD=60°,且FG∥CE,FG=CE,连接DB、DG,求出∠BDG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com