Question

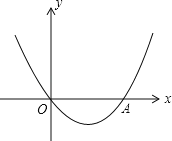
【题目】如图，抛物线y=x2+bx+c经过坐标原点，并与x轴交于点A（2，0）．

（1）求此抛物线的解析式；

（2）求此抛物线顶点坐标及对称轴；

（3）若抛物线上有一点B，且S△OAB=1，求点B的坐标．

Answer 1

【答案】（1）y=x2﹣2x；（2）抛物线的顶点坐标为（1，﹣1），对称轴为直线x=﹣1；（3）（1+，1）或（1﹣，1）或（1，﹣1）．

【解析】

试题分析：（1）利用交点式求抛物线解析式；

（2）把（1）中解析式配成顶点式即可得到抛物线顶点坐标及对称轴；

（3）设B（t，t2﹣2t），根据三角形面积公式得到×2×|t2﹣2t|=1，则t2﹣2t=1或t2﹣2t=﹣1，然后分别解两个方程求出t，从而可得到B点坐标．

解：（1）抛物线解析式为y=x（x﹣2），即y=x2﹣2x；

（2）因为y=x2﹣2x=（x﹣1）2﹣1，

所以抛物线的顶点坐标为（1，﹣1），对称轴为直线x=﹣1；

（3）设B（t，t2﹣2t），

因为S△OAB=1，

所以×2×|t2﹣2t|=1，

所以t2﹣2t=1或t2﹣2t=﹣1，

解方程t2﹣2t=1得t1=1+，t2=1﹣，则B点坐标为（1+，1）或（1﹣，1）；

解方程t2﹣2t=﹣1得t1=t2=1，则B点坐标为（1，﹣1），

所以B点坐标为（1+，1）或（1﹣，1）或（1，﹣1）．