
����Ŀ����ͼ����ABC�ı�BC��ֱ��l�ϣ�AC��BC����AC��BC����EFP�ı�FPҲ��ֱ��l�ϣ���EF���AC�غϣ���EF��FP.
(1)��ͼ���У�����ͨ���۲졢���������룬д��AB��AP�������������ϵ��λ�ù�ϵ��
(2)����EFP��ֱ��l����ƽ�Ƶ�ͼ�ڵ�λ��ʱ��EP��AC�ڵ�Q������AP��BQ�����벢д��BQ��AP�������������ϵ��λ�ù�ϵ����֤����IJ��룻
(3)����EFP��ֱ��l����ƽ�Ƶ�ͼ�۵�λ��ʱ��EP���ӳ��߽�AC���ӳ����ڵ�Q������AP��BQ������Ϊ(2)���������BQ��AP��������ϵ��λ�ù�ϵ��������������������֤����������������˵�����ɣ�

���𰸡�(1)AB��AP��AB��AP (2)BQ��AP��BQ��AP (3)����
��������
��1������ͼ�ξͿ��Բ�������ۣ���2��Ҫ֤BQ=AP������ת��Ϊ֤��Rt��BCQ��Rt��ACP��Ҫ֤��BQ��AP������֤����QMA=90����ֻҪ֤����1=��2����3=��4����1+��3=90������֤������3����ȣ�2����֤���Ϳ��Եõ��������Գ�����
(1)AB��AP��AB��AP
֤������AC��BC��AC=BC��
���ABCΪ����ֱ�������Σ�
���BAC=��ABC=![]() ��180�㩁��ACB��=45�㣬
��180�㩁��ACB��=45�㣬
�֡ߡ�ABC����EFPȫ�ȣ�
ͬ����֤��PEF=45�㣬
���BAP=45��+45��=90�㣬
��AB=AP��AB��AP��
��2��BQ=AP��BQ��AP��
֤����������֪����EF=FP��EF��FP��
���EPF=45�㣮
�֡�AC��BC��
���CQP=��CPQ=45�㣮
��CQ=CP��
����Rt��BCQ��Rt��ACP��
BC=AC����BCQ=��ACP=90�㣬CQ=CP��
���BCQ�ա�ACP��SAS����
��BQ=AP��
����ͼ���ӳ�BQ��AP�ڵ�M��
��Rt��BCQ��Rt��ACP��
���1=��2��
����Rt��BCQ�У���1+��3=90�����֡�3=��4��
���2+��4=��1+��3=90�㣮
���QMA=90�㣮
��BQ��AP��
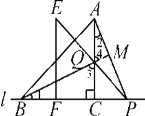
(3)������֤�����ߡ�EPF��45�㣬���CPQ��45��.�֡�AC��BC�����CQP����CPQ��45�㣬��CQ��CP.��SAS��֤��BCQ�ա�ACP����BQ��AP.�ӳ�QB��AP�ڵ�N�����PBN����CBQ.�ߡ�BCQ�ա�ACP�����BQC����APC.��Rt��BCQ�У���BQC����CBQ��90�㣬���APC����PBN��90�㣬���PNB��90�㣬��BQ��AP


 ����ѵ�����⿼ϵ�д�
����ѵ�����⿼ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϲ�����������⣮
��֪����һЩ�������ʽ������ƽ��ͼ�ε��������ʾ������(2a��b)(a��b)��2a2��3ab��b2�Ϳ�����ͼ���еĢٻ�ڵ������ʾ��
(1)��д��ͼ������ʾ�Ĵ������ʽ��
(2)����һ������ͼ�Σ�ʹ��������ܱ�ʾ(a��b)(a��3b)��a2��4ab��3b2��
(3)���������ʽ����дһ������a��b�Ĵ������ʽ����������֮��Ӧ�ļ���ͼ�Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ABCDE �ǡ�O ���ڽ�������Σ��ҡ�O �İ뾶Ϊ1����ͼ����Ӱ���ֵ�����ǣ� �� 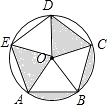
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���![]() ���������������ֱ����
���������������ֱ����![]() ��
��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
![]() ʹ��
ʹ��![]() ��
��![]() ���Ӷ���С��
���Ӷ���С��
![]() ʹ�ú���ͼ����
ʹ�ú���ͼ����![]() ��Ľ�����
��Ľ�����![]() ����Ϸ���
����Ϸ���
![]() ʹ�ú���ͼ��һ�����������ޣ�
ʹ�ú���ͼ��һ�����������ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��AEƽ��
��AEƽ��![]() ��
��![]() ����AC�ӳ�����F���Ҵ���ΪE�������н��ۣ�
����AC�ӳ�����F���Ҵ���ΪE�������н��ۣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ������ȷ�Ľ�����______
������ȷ�Ľ�����______![]() ��д���
����![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ��,��֪��A(O,1),B(1,2),��P��![]() �����˶�,����P��A��B����ľ���֮��ľ���ֵ���ʱ,�õ��Ϊ��P1,����P��A��B����ľ���֮����Сʱ,�õ��Ϊ��P2,��P1P2Ϊ�߳��������ε����Ϊ
�����˶�,����P��A��B����ľ���֮��ľ���ֵ���ʱ,�õ��Ϊ��P1,����P��A��B����ľ���֮����Сʱ,�õ��Ϊ��P2,��P1P2Ϊ�߳��������ε����Ϊ
A. 1 B. ![]() C.
C. ![]() D. 5
D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η���
��һԪ���η���![]()
(��)��֤:��������������ȵ�ʵ������
(��)���˷��̵�һ������1,��������̵���һ������
(��)����(��)����������Ϊ�߳��ĵ��������ε��ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CH����ǡ�ACD��ƽ���ߣ�BH�ǡ�ABC��ƽ���ߣ���A =58�������H�Ķ�����
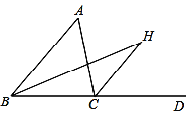
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���˸�2.2m��������֮��ľ���Ϊ1.6m����һ�����ӵ�����˨�����������ܽ�ϴ���������Ȼ�´���������״�� 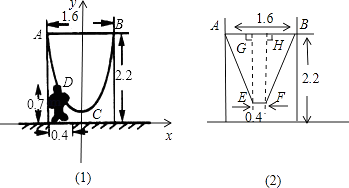
��1��һ����0.7m��С��վ��������0.4m������ͷ���պô������ӣ���������͵㵽����ľ��룻
��2��Ϊ�������Ǵ���ǧ�������Ӽ��Ϻ��м�ϵ��һ�鳤Ϊ0.4��ľ�壬����ϵľ����ȥ�����Ӻ����ߵ��������ø�Ϊ2�ף�ľ�������ƽ�У�����ʱľ�嵽����ľ��룮����ѡ�����ݣ� ![]() ��1.8��
��1.8�� ![]() ��1.9��
��1.9�� ![]() ��2.1��
��2.1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com