练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知五边形ABCDE 是⊙O 的内接正五边形，且⊙O 的半径为1．则图中阴影部分的面积是（ ）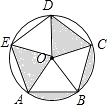
    A.
    B.
    C.
    D.

    【答案】B
    【解析】解：∵五边形ABCDE 是⊙O 的内接正五边形， ∴ = = = ，
    易知△EOA≌△AOB≌△BOC≌△COD，
    ∴△AOE、△AOB、△BOC、△COD的面积相等，
    ∴S阴=S扇形OAC
    =
    = π，
    故选B
    【考点精析】本题主要考查了正多边形和圆和扇形面积计算公式的相关知识点，需要掌握圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等；在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠DAB=∠ABC=90°，AB=BC，E是AB的中点，CE⊥BD．

    （1）求证：BE=AD；

    （2）求证：AC是线段ED的垂直平分线；

    （3）△DBC是等腰三角形吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．
    （1）求证：△COD是等边三角形；
    （2）当α=150°时，试判断△AOD的形状，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一艘轮船以30km/h的速度沿既定航线由南向北航行，途中接到台风警报，某台风中心正以10km/h的速度由东向西移动，距台风中心200km的圆形区域（包括边界）都属台风影响区，当这艘轮船接到台风警报时，它与台风中心的距离BC=500km，此时台风中心与轮船既定航线的最近距离AB=300km．

    （1）如果这艘船不改变航向，那么它会不会进入台风影响区？

    （2）如果你认为这艘轮船会进入台风影响区，那么从接到警报开始，经过多长时间它就会进入台风影响区？

    （3）假设轮船航向不变，轮船航行速度不变，求受到台风影响的时间为多少小时？

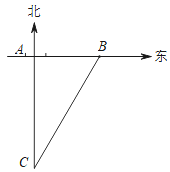
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，点D、E、F分别是边AB、AC、BC的中点，要判定四边形DBFE是菱形，下列所添加条件不正确的是（　　）

    A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在菱形ABCD中，∠ABC=60°，E是对角线AC上任意一点，F是线段BC延长线上一点，且CF=AE，连接BE、EF．

    （1）如图1，当E是线段AC的中点时，求证：BE=EF．

    （2）如图2，当点E不是线段AC的中点，其它条件不变时，请你判断（1）中的结论是否成立？若成立，请证明；若不成立，说明理由．

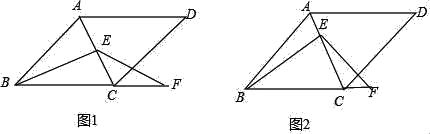
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系内，已知直线l1经过原点O 及A（2，2 ）两点，将直线l1向右平移4个单位后得到直线l2 ， 直线l2与x 轴交于点B．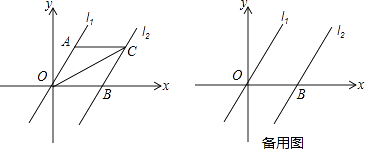
    （1）求直线l2的函数表达式；
    （2）作∠AOB 的平分线交直线l2于点C，连接AC．求证：四边形OACB是菱形；
    （3）设点P 是直线l2上一点，以P 为圆心，PB 为半径作⊙P，当⊙P 与直线l1相切时，请求出圆心P 点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的边BC在直线l上，AC⊥BC，且AC＝BC，△EFP的边FP也在直线l上，边EF与边AC重合，且EF＝FP.

    (1)在图①中，请你通过观察、测量、猜想，写出AB与AP所满足的数量关系和位置关系；

    (2)将△EFP沿直线l向左平移到图②的位置时，EP交AC于点Q，连接AP，BQ，猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想；

    (3)将△EFP沿直线l向左平移到图③的位置时，EP的延长线交AC的延长线于点Q，连接AP，BQ，你认为(2)中所猜想的BQ与AP的数量关系与位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解家长关注孩子成长方面的状况，学校开展了针对学生家长的“您最关心孩子哪方面成长”的主题调查，调查设置了“健康安全”、“日常学习”、“习惯养成”、“情感品质”四个项目，并随机抽取甲、乙两班共100位学生家长进行调查，根据调查结果，绘制了如图不完整的条形统计图．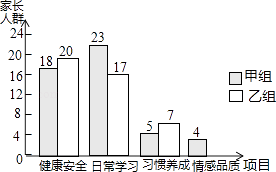
    （1）补全条形统计图．
    （2）若全校共有3600位学生家长，据此估计，有多少位家长最关心孩子“情感品质”方面的成长？
    （3）综合以上主题调查结果，结合自身现状，你更希望得到以上四个项目中哪方面的关注和指导？

    查看答案和解析>>

    同步练习册答案