
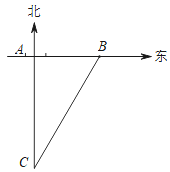
【题目】如图,一艘轮船以30km/h的速度沿既定航线由南向北航行,途中接到台风警报,某台风中心正以10km/h的速度由东向西移动,距台风中心200km的圆形区域(包括边界)都属台风影响区,当这艘轮船接到台风警报时,它与台风中心的距离BC=500km,此时台风中心与轮船既定航线的最近距离AB=300km.
(1)如果这艘船不改变航向,那么它会不会进入台风影响区?
(2)如果你认为这艘轮船会进入台风影响区,那么从接到警报开始,经过多长时间它就会进入台风影响区?
(3)假设轮船航向不变,轮船航行速度不变,求受到台风影响的时间为多少小时?
【答案】(1)如果这艘船不改变航向,那么它会进入台风影响区.(2)经过15﹣![]() h就会进入台风影响区;(3)2
h就会进入台风影响区;(3)2![]() 小时.
小时.
【解析】
(1)作出肯定回答:这艘轮船不改变航向,那么它能进入台风影响区.
(2)首先假设轮船能进入台风影响区,进而利用勾股定理得出等式求出即可.
(3)将轮船刚好进入台风影响区和刚好离开台风影响的两个时间节点相减,即能得出受影响的时间长.
解:(1)如图易知AB′=300﹣10t,AC′=400﹣30t,

当B′C′=200时,将受到台风影响,
根据勾股定理可得:(300﹣10t)2+(400﹣30t)2=2002,
整理得到:t2﹣30t+210=0,
解得t=15±![]() ,
,
由此可知,如果这艘船不改变航向,那么它会进入台风影响区.
(2)由(1)可知经过(15﹣![]() )h就会进入台风影响区;
)h就会进入台风影响区;
(3)由(1)可知受到台风影响的时间为:15+![]() ﹣(15﹣
﹣(15﹣![]() )=2
)=2![]() h.
h.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】阅读材料并解答下列问题.
你知道吗?一些代数恒等式可以用平面图形的面积来表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图甲中的①或②的面积表示.
(1)请写出图乙所表示的代数恒等式;
(2)画出一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)请仿照上述式子另写一个含有a,b的代数恒等式,并画出与之对应的几何图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).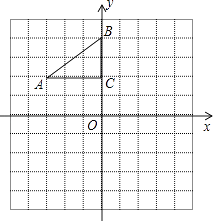
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(3,0),B(0,4),则点B100的坐标为 . 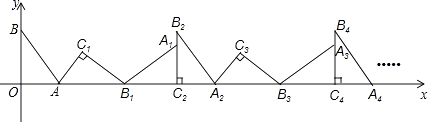
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ![]() ,
, ![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.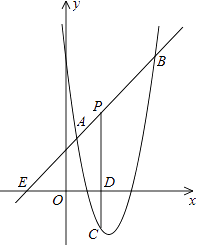
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com