
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△ACD,连接AD,BC.若∠ACB=30°,AB=1,CC=x,则下列结论:①△AAD≌△CCB;②当x=1时,四边形ABCD是菱形;③当x=2时,△BDD为等边三角形.其中正确的是_______(填序号).

科目:初中数学 来源: 题型:
【题目】为了增强学生的身体素质,某校坚持常年的全员体育锻炼,并定期进行体能测试.下面将某班学生立定跳远成绩(精确到0.1m)进行整理后,分成5组(含低值不含高值):1.60~1.80,1.80~2.00,2.00~2.20,2.20~2.40,2.40~2.60,已知前4个小组的频率分别是0.05,0.15,0.30,0.35,第五个小组的频数是9.
(1)该班参加这项测试的人数是多少人?
(2)请画出频数分布直方图.
(3)成绩在2.00米以上(含2.00米)为合格,则该班成绩的合格率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
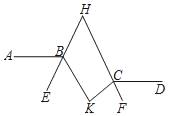
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
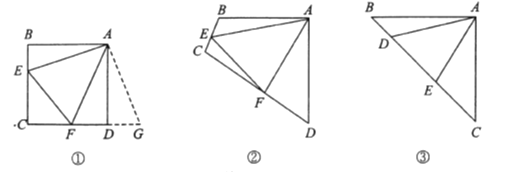
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上, ![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.
(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上, ![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中, ![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com