
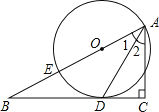
【题目】如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…,由此可发现:![]() ,
,![]() ,
,![]() ,…,请写出第6个数组:__.
,…,请写出第6个数组:__.
查看答案和解析>>
科目:初中数学 来源: 题型:
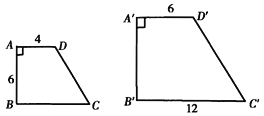
【题目】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
(1)梯形ABCD与梯形A′B′C′D′的相似比k;
(2)A′B′和BC的长;
(3)D′C′∶DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解答下列问题:
题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式=
,则原式=![]()
![]()
再将“![]() ”还原,得原式=
”还原,得原式=![]() .
.
上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你仿照上面的方法解答下列问题:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求证:若![]() 为正整数,则式子
为正整数,则式子![]() 的值一定是某一个正整数的平方.
的值一定是某一个正整数的平方.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
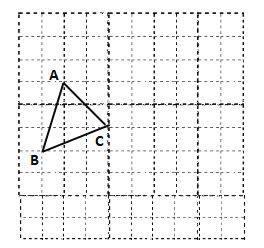
【题目】如图,在边长为1的小正方形组成的10×10网络中(我们把组成网格的小正方形的顶点称为格点),△ABC的三个顶点分别在网格的格点上
(1)请你在所给的网格中建立平面直角坐标系,使△ABC的顶点A的坐标为(-3,5);
(2)在(1)的坐标系中,直接写出△ABC其它两个顶点的坐标;
(3)在(1)的坐标系中,画出△ABC关于y轴对称的图形△A1B1C1 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() OABC的顶点O,A,C的坐标分别是(0,0),(2,0),(
OABC的顶点O,A,C的坐标分别是(0,0),(2,0),(![]() ,1),则点B的坐标是( )
,1),则点B的坐标是( )
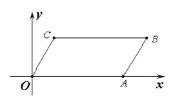
A.(1,2)B.(![]() ,2)C.(
,2)C.(![]() ,1)D.(3,1)
,1)D.(3,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com