
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
【答案】(1)A型芯片的单价为26元/条,B型芯片的单价为35元/条;(2)80.
【解析】
(1)设B型芯片的单价为x元/条,则A型芯片的单价为(x﹣9)元/条,根据数量=总价÷单价结合用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购买a条A型芯片,则购买(200﹣a)条B型芯片,根据总价=单价×数量,即可得出关于a的一元一次方程,解之即可得出结论.
(1)设B型芯片的单价为x元/条,则A型芯片的单价为(x﹣9)元/条,根据题意得:
![]() ,
,
解得:x=35,
经检验,x=35是原方程的解,
∴x﹣9=26.
答:A型芯片的单价为26元/条,B型芯片的单价为35元/条.
(2)设购买a条A型芯片,则购买(200﹣a)条B型芯片,根据题意得:
26a+35(200﹣a)=6280,
解得:a=80.
答:购买了80条A型芯片.


科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导“节约用水,从我做起”,市政府决定对市直机关500户家庭的用水情况做一次调查,市政府调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨)并将调查结果制成了如图所示的条形统计图。
(1)请将条形统计图补充完整;
(2)求这100个样本数据的平均数,众数和中位数;
(3)根据样本数据,估计市直机关500户家庭中平均用水量不超过12吨的约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线经过点A(0,2)、点B(1,0),将这条直线向左平移与x轴、y轴分别交与点C、点D.若DB=DC,则直线CD的函数解析式为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
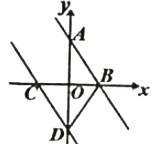
【题目】阅读:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为![]() ,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
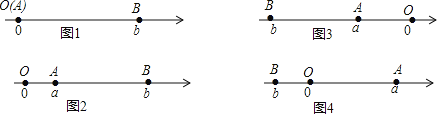
当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列问题:
(1)数轴上表示3和5的两点之间的距离是_________,数轴上表示-3和-5的两点之间的距离是_________,数轴上表示1和-2的两点之间的距离是 ;
(2)数轴上表示x和-1的两点A和B之间的距离是 ,如果∣AB∣=3,那么x为 ;
(3)当代数式∣x+3∣+∣x-2∣取最小值时,相应的x的取值范围是 ;当![]() 为 时,该代数式为7.
为 时,该代数式为7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…则第n个图形有__个小圆.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
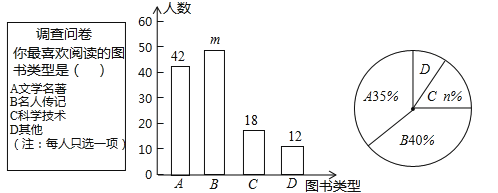
(1)本次调查共抽查了 名学生;
(2)两幅统计图中的m= ,n= .
(3)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直接写出结果:
(1)6+(﹣9)=_____.
(2)﹣5﹣15=____.
(3)12÷(﹣3)=____.
(4)![]() =______.
=______.
(5)![]() =______.
=______.
(6)(﹣2)2018+(﹣2)2017=______.
(7)﹣3a2+2a2=_____.
(8)﹣2(x﹣1)=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com