
【题目】阅读:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为![]() ,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
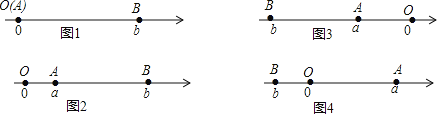
当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;如图3,点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;如图4,点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列问题:
(1)数轴上表示3和5的两点之间的距离是_________,数轴上表示-3和-5的两点之间的距离是_________,数轴上表示1和-2的两点之间的距离是 ;
(2)数轴上表示x和-1的两点A和B之间的距离是 ,如果∣AB∣=3,那么x为 ;
(3)当代数式∣x+3∣+∣x-2∣取最小值时,相应的x的取值范围是 ;当![]() 为 时,该代数式为7.
为 时,该代数式为7.
【答案】(1)2,2,3;(2)![]() ,2或-4;(3)
,2或-4;(3)![]() ,-4或3.
,-4或3.
【解析】
(1)(2)根据数轴上A、B两点之间的距离![]() ,代入数值即可求出;
,代入数值即可求出;
(3)代数式![]() 的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,据此即可求出x的范围;若
的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,据此即可求出x的范围;若![]() ,在中间的时候代数式的值是5,只要在-3的左侧和2的右侧各找到一个到最近点距离为1的点就是所求.
,在中间的时候代数式的值是5,只要在-3的左侧和2的右侧各找到一个到最近点距离为1的点就是所求.
解:(1)数轴上表示3和5的两点之间的距离是![]() ;
;
数轴上表示-3和-5的两点之间的距离是![]() ;
;
数轴上表示1和-2的两点之间的距离是![]() ;
;
(2)数轴上表示x和-1的两点A和B之间的距离是![]() ;
;
如果![]() ,则
,则![]() ,所以
,所以![]() 或
或![]() ,解得:x=2或-4;
,解得:x=2或-4;
(3)代数式![]() 的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,那么x应在-3与2之间的线段上,所以
的最小值,意思是数轴上数x到-3的距离与到2 的距离之和最小,那么x应在-3与2之间的线段上,所以![]() ,这个最小值是
,这个最小值是![]() ;
;
若![]() ,在
,在![]() 时,
时,![]() =5,所以只要在数轴上-3的左侧和2的右侧各找到一个到-3的距离和到2的距离为1的点就是所求,在数轴上-3的左侧的数是-4,2的右侧的数是3,所以当x=-4或3时,
=5,所以只要在数轴上-3的左侧和2的右侧各找到一个到-3的距离和到2的距离为1的点就是所求,在数轴上-3的左侧的数是-4,2的右侧的数是3,所以当x=-4或3时,![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】(1)如图1,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.求线段
的中点.求线段![]() 的长;
的长;
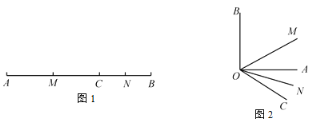
(2)点![]() 在线段
在线段![]() 上,若
上,若![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.你能得出
的中点.你能得出![]() 的长度吗?并说明理由.
的长度吗?并说明理由.
(3)类似的,如图2,![]() 是直角,射线
是直角,射线![]() 在
在![]() 外部,且
外部,且![]() 是锐角,
是锐角,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.当
的平分线.当![]() 的大小发生改变时,
的大小发生改变时,![]() 的大小也会发生改变吗?为什么?
的大小也会发生改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上![]() 、
、![]() 两点分别表示有理数
两点分别表示有理数![]() 和
和![]() ,我们用
,我们用![]() 表示
表示![]() 到
到![]() 之间的距离;例如
之间的距离;例如![]() 表示7到3之间的距离.
表示7到3之间的距离.
(1)当![]() 时,
时,![]() 的值为 .
的值为 .
(2)如何理解![]() 表示的含义?
表示的含义?
(3)若点![]() 、
、![]() 在0到3(含0和3)之间运动,求
在0到3(含0和3)之间运动,求![]() 的最小值和最大值.
的最小值和最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司 | 单价(元/半小时) | 充值优惠 |
A | m | 充20元送5元,即:充20元实得25元 |
B | m-0.2 | 无 |
C | 1 | 充20元送20元,即:充20元实得40元 |
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,直线l1经过(2,3)和(-1,-3):直线l2经过原点O,且与直线l1交于点P(-2,a).
(1)求a的值;
(2)(-2,a)可看成怎样的二元一次方程组的解?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
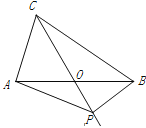
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com