
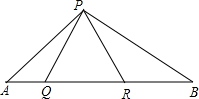
 如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9.
如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9. 分析 利用等边三角形性质,进一步证得△AQP∽△PRB,再由三角形相似的性质解答即可.
解答 证明:∵△PQR是等边三角形,
∴QR=PQ=PR,∠PQR=∠PRQ=∠QPR=60°,
∴∠AQP=∠PRB=120°,
∴∠A+∠APQ=60°,
又∵∠APB=120°,
∴∠A+∠B=60°,
∴∠APQ=∠B,
∴△AQP∽△PRB,
∴$\frac{PQ}{BR}=\frac{AQ}{PR}$,
∵QR=PQ=PR,
∴QR2=AQ•BR,
∴BR=$\frac{Q{R}^{2}}{AQ}$=$\frac{{6}^{2}}{4}$=9;
故答案为:9.
点评 此题主要考查等边三角形的性质,三角形相似的判定与性质以及等量代换的渗透;证明三角形相似是解决问题的关键.


科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列命题正确的是( )
①三角形中最大内角一定不小于600;
② 所有等腰直角三角形都相似;
③正多边形的外角为240,则它的中心角也为240;
④顺次连接对角线相等的四边形各边中点得到矩形.
A. ①② B. ①②③ C. ②③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市八年级3月调研考试数学试卷(解析版) 题型:解答题
如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P开始从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm,点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间我t秒.
(1)出发2秒后,求PQ的长;
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,则求出几秒后第一次形成等腰三角形;若不能,则说明理由;
(3)从出发几秒后,线段PQ第一次把直角三角形周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
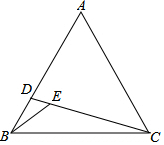 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
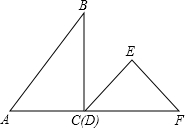 一副三角板如图摆放,AC、DF在同一条直线上且点C、D重合,将三角板DEF沿CA方向以1cm/s的速度运动,当点D与点A重合时运动停止,已知AC=3cm,DF=4cm,设运动的时间为t(s),两三角板重合部分的面积为S(cm2),下列图象能大致反映S(cm2)与t(s)间函数关系的是( )
一副三角板如图摆放,AC、DF在同一条直线上且点C、D重合,将三角板DEF沿CA方向以1cm/s的速度运动,当点D与点A重合时运动停止,已知AC=3cm,DF=4cm,设运动的时间为t(s),两三角板重合部分的面积为S(cm2),下列图象能大致反映S(cm2)与t(s)间函数关系的是( )| A. | 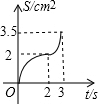 | B. | 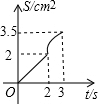 | C. | 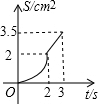 | D. | 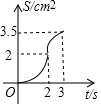 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com