
【题目】你能化简(x-1)(x99+x98+x97+…+x+1)吗?遇到这样的问题,我们可以先从简单的情形入手:
分别计算下列各式的值:
①(x-1)(x+1)=x2-1;
②(x-1)(x2+x+1)=x3-1;
③(x-1)(x3+x2+x+1)=x4-1;…
由此我们可以得到:(x-1)(x99+x98+x97+…+x+1)=________________;
请你利用上面的结论,完成下面三题的计算:
⑴299+298+297+…+2+1;
⑵(-2)50+(-2)49+(-2)48+…+(-2)+1
⑶已知![]() ,求
,求![]() 的值.
的值.
【答案】x100﹣1;(1)2100﹣1;(2)![]() ;(3)1.
;(3)1.
【解析】试题分析:根据所给出的式子找出规律,根据规律得出答案;(1)、在式子的前面添加(2-1),从而根据规律得出答案;(2)、在等式的前面添加![]() ×(﹣2﹣1),然后利用简便方法进行计算得出答案;(3)、根据题意得出(x﹣1)(x3+x2+x+1)=0,即x4﹣1=0,从而求出x的值,然后代入进行计算得出答案.
×(﹣2﹣1),然后利用简便方法进行计算得出答案;(3)、根据题意得出(x﹣1)(x3+x2+x+1)=0,即x4﹣1=0,从而求出x的值,然后代入进行计算得出答案.
试题解析:观察所给等式可得(x﹣1)(x99+x98+x97+…+x+1)=x100﹣1,
(1)、299+298+297+…+2+1=(2﹣1)(299+298+297+…+2+1)=2100﹣1;
(2)、∵原式=![]() ×(﹣2﹣1)[+(﹣2)50+(﹣2)49+…+(﹣2)+1]=
×(﹣2﹣1)[+(﹣2)50+(﹣2)49+…+(﹣2)+1]= ![]() ×[ (﹣2)51﹣1]=
×[ (﹣2)51﹣1]= ![]() ,
,
(3)、∵x3+x2+x+1=0, ∴(x﹣1)(x3+x2+x+1)=0,即x4﹣1=0,
解得:x=1(不合题意,舍去)或x=﹣1,
则x2008=(﹣1)2008=1.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列事件发生的概率,把A,B,C,D填入事件后的括号里.
A.发生的概率为0 B.发生的概率小于![]()
C.发生的概率大于![]() D.发生的概率为1
D.发生的概率为1
(1)从一副扑克牌中任意抽取一张,是红桃;( )
(2)2024年2月有29天;( )
(3)小波能举起500 kg的大石头;( )
(4)从5张分别写有数字1,2,4,6,8的卡片中任取一张,卡片上数字恰为偶数.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,坐标原点O为矩形ABCD的对称中心,顶点A的坐标为(1,t),AB∥x轴,矩形A′B′C′D′与矩形ABCD是位似图形,点O为位似中心,点A′,B′分别是点A,B的对应点,![]() .已知关于x,y的二元一次方程
.已知关于x,y的二元一次方程![]() (m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )
(m,n是实数)无解,在以m,n为坐标(记为(m,n)的所有的点中,若有且只有一个点落在矩形A′B′C′D′的边上,则kt的值等于( )

A.![]() B.1 C.
B.1 C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数![]() 的图象有一个交点为A(m,2).
的图象有一个交点为A(m,2).
(1)求m的值及正比例函数y=kx的表达式;
(2)试判断点B(2,3)是否在正比例函数图象上,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
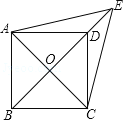
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图:
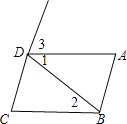
![]() 若
若![]() ,
,
则______ ![]() ______
______ ![]() 内错角相等,两直线平行
内错角相等,两直线平行![]() ;
;
若![]() ,
,
则______ ![]() ______
______ ![]() 同旁内角互补,两直线平行
同旁内角互补,两直线平行![]() ;
;
![]() 当______
当______ ![]() ______ 时,
______ 时,
![]() 两直线平行,同旁内角互补
两直线平行,同旁内角互补![]() ;
;
![]() 当______
当______ ![]() ______ 时,
______ 时,
![]()
![]() 两直线平行,同位角相等
两直线平行,同位角相等![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]()
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;
(3)现规定:摸到红球得5分,摸到黄球得3分,摸到蓝球得2分(每次摸后放回),乙同学在一次摸球游戏中,第一次随机摸到一个红球第二次又随机摸到一个蓝球,若随机再摸一次,求乙同学三次摸球所得分数之和不低于10分的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
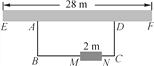
【题目】如图,利用一面墙(墙EF最长可利用28米),围成一个矩形花园ABCD.与墙平行的一边BC上要预留2米宽的入口(如图中MN所示,不用砌墙).现有砌60米长的墙的材料.
(1)当矩形的长BC为多少米时,矩形花园的面积为300平方米;
(2)能否围成480平方米的矩形花园,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com