
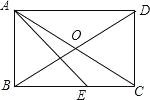
【题目】如图,在矩形ABCD中,AE平分∠BAD交BC于点E,CE=1,∠CAE=15°,则BE等于
【答案】![]()
【解析】
试题分析:由矩形ABCD,得到OA=OB,根据AE平分∠BAD,得到等边三角形OA=OB和△ABE是等腰直角三角形,求出∠BAO,最后用勾股定理计算即可.
∵四边形ABCD是矩形, ∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°, ∴OA=OB,∠DAE=∠AEB,∵AE平分∠BAD, ∴∠BAE=∠DAE=45°=∠AEB, ∴AB=BE, ∵∠CAE=15°,
∴∠DAC=45°﹣15°=30°, ∠BAC=60°, ∴△BAO是等边三角形, ∴AB=OB,∠BAO=60°,
在RT△ABC中,BC=AB+CE=AB+1, ∴tan∠BAC=![]() =
=![]() =tan60°=
=tan60°=![]() , ∴AB=
, ∴AB=![]() ,
,
∴BE=AB=![]() ,
,



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小红和小明在研究一个数学问题:已知AB∥CD,AB和CD都不经过点E,探索∠E与∠A,∠C的数量关系. 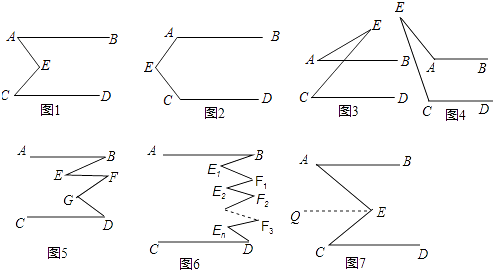
(1)发现:在图1中,小红和小明都发现:∠AEC=∠A+∠C; 小红是这样证明的:如图7过点E作EQ∥AB.
∴∠AEQ=∠A()
∵EQ∥AB,AB∥CD.
∴EQ∥CD()
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C 即∠AEC=∠A+∠C.
小明是这样证明的:如图7过点E作EQ∥AB∥CD.
∴∠AEQ=∠A,∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C即∠AEC=∠A+∠C
请在上面证明过程的横线上,填写依据:
两人的证明过程中,完全正确的是 .
(2)尝试: ①在图2中,若∠A=110°,∠C=130°,则∠E的度数为;
②在图3中,若∠A=20°,∠C=50°,则∠E的度数为 .
(3)探索: 装置图4中,探索∠E与∠A,∠C的数量关系,并说明理由.
(4)猜想: 如图5,∠B、∠D、∠E、∠F、∠G之间有什么关系?(直接写出结论)
(5)如图6,你可以得到什么结论?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
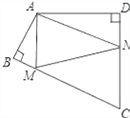
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位运动员在一段2000米长的笔直公路上进行跑步比赛,比赛开始时甲在起点,乙在甲的前面200米,他们同时同向出发匀速前进,甲的速度是8米/秒,乙的速度是6米/秒,先到终点者在终点原地等待.设甲、乙两人之间的距离是y米,比赛时间是x秒,当两人都到达终点计时结束,整个过程中y与之间的函数图象是( )
A.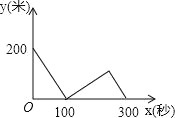 B.
B.
C.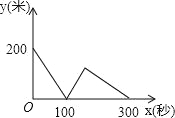 D.
D.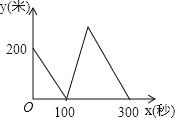
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com