
【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽为8米(即AB=8米),拱顶高出水面为2米(即CD=2米).
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽6米,船舱顶部为正方形并高出水面1.5米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.

【答案】(1)r=5;(2)货船不可以顺利通过这座拱桥.
【解析】
(1)连接OA,设这座拱桥所在圆的半径为r米,由垂径定理可得AD=![]() AB=4,在Rt△AOD中,根据勾股定理得方程r2=42+(r-2)2,解此方程即可求得答案;(2)连接OM,设MN=5,根据勾股定理求得OH的长,即可求得HD的长,与1.5米比较,即可得到此时货船能否顺利通过这座拱桥.
AB=4,在Rt△AOD中,根据勾股定理得方程r2=42+(r-2)2,解此方程即可求得答案;(2)连接OM,设MN=5,根据勾股定理求得OH的长,即可求得HD的长,与1.5米比较,即可得到此时货船能否顺利通过这座拱桥.
(1)连接OA ,

设OA=r,则OD=OC-CD=r-2,AD=![]() AB=4,
AB=4,
在Rt△AOD中,∵OA2=AD2+OD2,
∴r2=42+(r-2)2
∴r=5 .
(2)货船不能顺利通过这座拱桥.理由:
连接OM,由题意可知MN=6米,

∵OC⊥MN,
∴MH=![]() MN=3米,
MN=3米,
在Rt△OMH中,OH=![]() =4米,
=4米,
∵OD=OC-CD=5-2=3米
∵DH=OH-OD=4-3=1米<1.5米,
∴货船不能顺利通过这座拱桥.


科目:初中数学 来源: 题型:
【题目】已知边长为2的正六边形ABCDEF在平面直角坐标系中的位置如图所示,点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2018次翻转之后,点B的坐标是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象经过点
的图象经过点![]() ,且与正比例函数
,且与正比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
(1)求m的值;
(2)求一次函数![]() 的解析式;
的解析式;
(3)求这两个函数图象与x轴所围成的三角形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,且垂足H在边AD上,连接AF.
(1)求证:FH=ED;
(2)设AE=x,是否存在某个x的值,使得△AEF的面积为3?若存在,求出x的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
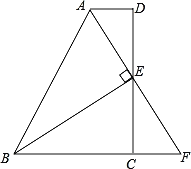
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2.其中正确的是( )

A. ①②③④ B. ②④ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕将△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个登山爱好者经常相约去登山,今年1月甲参加了两次登山活动.
(1)1月1日甲与乙同时开始攀登一座900米高的山,甲的平均攀登速度是乙的1.2倍,结果甲比乙早15分钟到达顶峰.求甲的平均攀登速度是每分钟多少米?
(2)1月6日甲与丙去攀登另一座h米高的山,甲保持第(1)问中的速度不变,比丙晚出发0.5小时,结果两人同时到达顶峰,问甲的平均攀登速度是丙的多少倍?(用含h的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com