解:(1)过点M作MC
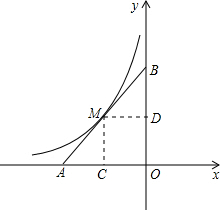
⊥x轴,MD⊥y轴,
∵AM=BM,
∴点M为AB的中点,
∵MC⊥x轴,MD⊥y轴,
∴MC∥OB,MD∥OA,
∴点C和点D分别为OA与OB的中点,
∴MC=MD,
则点M的坐标可以表示为(-a,a),
把M(-a,a)代入函数y=
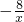
中,
解得a=2

,
则点M的坐标为(-2

,2

);
(2)∵则点M的坐标为(-2

,2

),
∴MC=2

,MD=2

,
∴OA=OB=2MC=4

,
∴A(-4

,0),B(0,4

),
设直线AB的解析式为y=kx+b,
把点A(-4

,0)和B(0,4

)分别代入y=kx+b中得
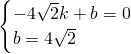
,
解得:
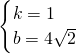
.
则直线AB的解析式为y=x+4

.
分析:(1)过点M作MC⊥x轴,MD⊥y轴,根据M为AB的中点,MC∥OB,MD∥OA,利用平行线分线段成比例得到点C和点D分别为OA与OB的中点,从而得到MC=MD,设出点M的坐标代入反比例函数解析式中,求出a的值即可得到点M的坐标;
(2)根据(1)中求出的点M的坐标得到MC与MD的长,从而求出OA与OB的长,得到点A与点B的坐标,设出一次函数的解析式,把点A与点B的坐标分别代入解析式中求出k与b的值,确定出直线AB的表达式.
点评:此题考查了反比例函数与一次函数的交点问题,平行线分线段成比例,以及中位线定理,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

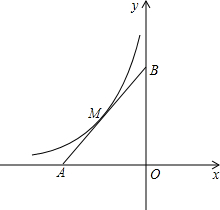 已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=
已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数y=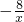 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM. ⊥x轴,MD⊥y轴,
⊥x轴,MD⊥y轴,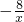 中,
中, ,
, ,2
,2 );
); ,2
,2 ),
), ,MD=2
,MD=2 ,
, ,
, ,0),B(0,4
,0),B(0,4 ),
), ,0)和B(0,4
,0)和B(0,4 )分别代入y=kx+b中得
)分别代入y=kx+b中得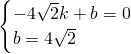 ,
,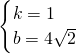 .
. .
.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=