
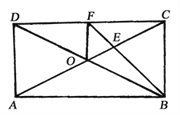
【题目】如图,已知矩形ABCD的对角线AC、BD交于O点,∠ABC的平分线交AC于E,交CD于F,∠DBF=15°,连结OF,则下列三角形①△AOD,②△COF,③△DOF,④△EOF中是等腰三角形的为________(填入序号)。
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | a | 40% |
1200≤x<1400 | 9 | 22.5% |
1400≤x<1600 | b | c |
1600≤x<1800 | 2 | 5% |
合计 | 40 | 100% |
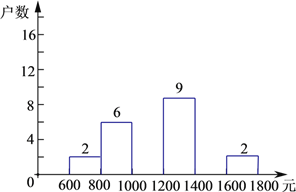
根据以上提供的信息,解答下列问题:
(1)频数分布表中:a= ,b= ,c= .
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
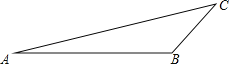
【题目】小红同学要测量A、C两地的距离,但A、C之间有一水池,不能直接测量,于是她在A、C同一水平面上选取了一点B,点B可直接到达A、C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A、C两点之间的距离.(参考数据![]() ≈4.5,
≈4.5, ![]() ≈4.6)
≈4.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )
A. ①②③ B. ①③④ C. ②③ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个样本有50个数据,其中最大值是208,最小值是169,最大值与最小值的差是______;如果取组距为5,那么这组数据应分成______组,第一组的起点为________,第二组与第一组的分点为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两组数据:a1,a2,a3,a4,a5和a1-1,a2-1,a3-1,a4-1,a5-1,下列判断中错误的是( )
A. 平均数不相等,方差相等 B. 中位数不相等,标准差相等
C. 平均数相等,标准差不相等 D. 中位数不相等,方差相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲。如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10 x元(x为整数)。
(1)(2分)直接写出每天游客居住的房间数量y与x的函数关系式。
(2)(4分)设宾馆每天的利润为W元,当每间房价定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)(4分)某日,宾馆了解当天的住宿的情况,得到以下信息:①当日所获利润不低于5000元,②宾馆为游客居住的房间共支出费用没有超过600元,③每个房间刚好住满2人。问:这天宾馆入住的游客人数最少有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com