


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与点C重合,再展开,折痕EF交AD边于点E,交BC边于点F,分别连结AF和CE.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 3 |
| 1 |
| x-1 |
| 1 |
| x+1 |
| x |
| 2x2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
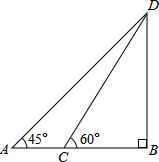 某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(
某校数学兴趣小组测量一座大桥高度,如图所示,他们在A处测得大桥最高点D的仰角为45°,在前方240m的C处测得大桥最高点D的仰角为60°,求该兴趣小组测得的大桥高度DB.(| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com