
【题目】如图所示,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() 和
和![]() 的面积分别为49,40,则
的面积分别为49,40,则![]() 的面积为( )
的面积为( )
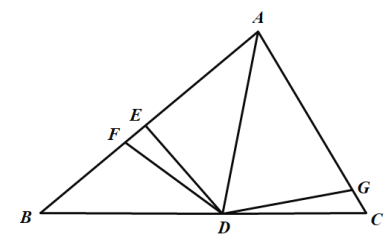
A.3.5B.4.5C.9D.10
【答案】B
【解析】
根据题意作DM=DE交AC于M,作DN⊥AC,构造全等三角形利用全等三角形的判定及性质以及角平分线的性质进行分析求解.
解:作DM=DE交AC于M,作DN⊥AC,
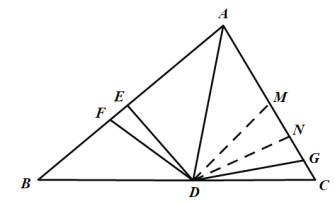
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DN,
在Rt△DEF和Rt△DMN中,
![]()
∴Rt△DEF≌Rt△DMN(HL),
∵DE=DG,DM=DE,
∴DM=DG,
∵DN⊥AC,
在Rt△DGN和Rt△DMN中,
![]()
∴Rt△DGN≌Rt△DMN(HL),
在Rt△DFA和Rt△DNA中,
![]()
∴Rt△DFA≌Rt△DNA(HL),
∴Rt△AED≌Rt△AMD,
∵△ADG和△AED的面积分别为49和40,
∴S△MDG=S△ADG-S△ADM=49-40=9,
S△DNM=S△DEF=![]() S△MDG=
S△MDG=![]() ×9=4.5.
×9=4.5.
故选:B.


科目:初中数学 来源: 题型:
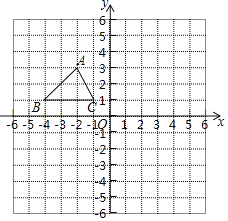
【题目】△ABC在直角坐标系中的位置如图,其中A点的坐标是(﹣2,3)
(1)△ABC绕点O顺时针旋转90°得到△A1B1C1,请作出△A1B1C1,并写出A点的对应点A1的坐标;
(2)若△ABC经过平移后A点的对应点A2的坐标是(2,﹣1),请作△A2B2C2,并计算平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,
(1)如图1,①线段![]() 和
和![]() 的数量关系是__________;
的数量关系是__________;
②请写出线段![]() ,
,![]() ,
,![]() 之间的数量关系并证明.
之间的数量关系并证明.
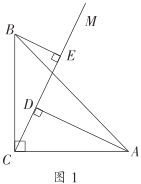
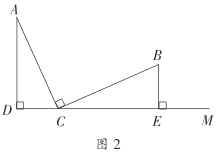
(2)如图2,若已知条件不变,上述结论②还成立吗?如果不成立,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在规格为8×8的边长为1个单位的正方形网格中(每个小正方形的边长为1),△ABC的三个顶点都在格点上,且直线m、n互相垂直.
(1)画出△ABC关于直线n的对称图形△A′B′C′;
(2)直线m上存在一点P,使△APB的周长最小;
①在直线m上作出该点P;(保留画图痕迹)
②△APB的周长的最小值为 .(直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上, 且
上, 且![]() .
.
(1)求证:![]() 为等腰直角三角形;
为等腰直角三角形;
(2)若![]() 的面积为7,求四边形
的面积为7,求四边形![]() 的面积;
的面积;
(3)如图(2),如果点![]() 运动到
运动到![]() 的延长线上时,点
的延长线上时,点![]() 在射线
在射线![]() 上且保持
上且保持![]() ,
,![]() 还是等腰直角三角形吗.请说明理由.
还是等腰直角三角形吗.请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
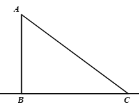
【题目】如图,在Rt△ABC中,AB=3,BC=4,AC=5,在直线BC上有P点,使△PAC是以AC为腰的等腰三角形,则BP的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 边上的中点.
边上的中点.
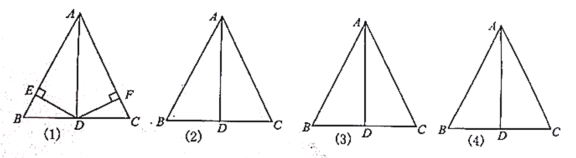
(1)若![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .判断
.判断![]() 的形状,并证明;
的形状,并证明;
(2)若![]() 分别是
分别是![]() 上的中线,连接
上的中线,连接![]() .判断
.判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)若![]() 分别是
分别是![]() 的平分线,连接
的平分线,连接![]() .判断
.判断![]() 的关系,不需证明;
的关系,不需证明;
(4)若分别在![]() 上任取一点
上任取一点![]() ,且
,且![]() ,连接
,连接![]() .在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
.在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com