
分析 (1)设A、B两种型号背包的进货单价各为x元、y元,根据用2200元同时购进A、B两种型号背包个40个,购进A型背包2个比购进B型背包1个多用20元,列方程组求解;
(2)设商场用于批发的背包数量为a个,根据总获利不低于1350元,列不等式,求出最大整数解.
解答 解:(1)设A型背包每个为x元,B型背包每个为y元,由题意得
$\left\{\begin{array}{l}{40x+40y=2200}\\{2x-y=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=25}\\{y=30}\end{array}\right.$.
答:A、B两种型号背包的进货单价各为25元、30元;
(2)设商场用于让利销售的背包数量为a个,
由题意得,50×70%a+50(40×2-a)-2200≥1350,
解得:a≤30.
所以,商场用于让利销售的背包数数量最多为30个.
答:商场用于让利销售的背包数数量最多为30个.
点评 本题考查了二元一次方程组和一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列方程组和不等式求解.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
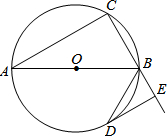 已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于点D,DE⊥CB的延长线于点E.
已知:如图,AB是⊙O的直径,点C在⊙O上,△ABC的外角平分线BD交⊙O于点D,DE⊥CB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )| A. | 12m | B. | 3$\sqrt{3}$m | C. | 4$\sqrt{3}$m | D. | 12$\sqrt{3}$m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com