
【题目】以点A为顶点作等腰Rt△ABC,等腰Rt△ADE,其中∠BAC=∠DAE=90°,如图1所示放置,使得一直角边重合,连接BD、CE.

(1)试判断BD、CE的数量关系,并说明理由;
(2)延长BD交CE于点F试求∠BFC的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
【答案】(1)CE=BD,理由见解析;(2)90°;(3)成立,理由见解析
【解析】
试题分析:(1)根据SAS证明△EAC与△DAB全等,再利用全等三角形的性质解答即可;
(2)利用全等三角形的性质得出∠ECA=∠DBA,进而解答即可;
(3)根据(1)(2)中的证明步骤解答即可.
解:(1)CE=BD,理由如下:
∵等腰Rt△ABC,等腰Rt△ADE,
∴AE=AD,AC=AB,
在△EAC与△DAB中,
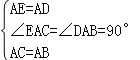 ,
,
∴△EAC≌△DAB(SAS),
∴CE=BD;
(2)∵△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECA+∠CBF=∠DBA+∠CBF=45°,
∴∠ECA+∠CBF+∠DCB=45°+45°=90°,
∴∠BFC=180°﹣90°=90°;
(3)成立,
∵等腰Rt△ABC,等腰Rt△ADE,
∴AE=AD,AC=AB,
在△EAC与△DAB中,
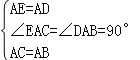 ,
,
∴△EAC≌△DAB(SAS),
∴CE=BD;
∵△EAC≌△DAB,
∴∠ECA=∠DBA,
∴∠ECA+∠CBF=∠DBA+∠CBF=45°,
∴∠ECA+∠CBF+∠DCB=45°+45°=90°,
∴∠BFC=180°﹣90°=90°.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3) 若分别以直角三角形ABC三边为边向外作三个正多边形,其面积分别用S1、S2、S3表示,请你猜想S1、S2、S3之间的关系?.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知网格上最小的正方形的边长为1,
(1)作△ABC关于![]() 轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于
轴的对称图形△A'B'C'(不写做法),并写出A'B'C'的坐标,想一想:关于![]() 轴对称的两个点之间有什么关系?
轴对称的两个点之间有什么关系?
(2)求△ABC的面积.
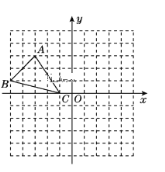
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解南通市80万市民“获取新闻的最主要途径”,某市记者开展了一次调查,根据调查结果绘制了如下尚不完整的统计图.
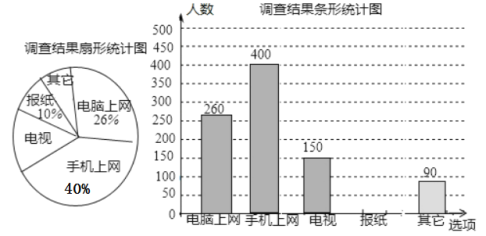
根据以上信息解答下列问题:
(1)这次调查适合采用_____________的调查方式(填“全面调查”或“抽样调查”);
(2)这次调查样本容量是____________.
(3)扇形统计图中,“电视”所对应的圆心角的度数是____________;
(4)条形统计图中“报纸”对应的人数是____________;
(5)南通市约有80万人,请估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
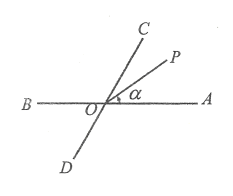
【题目】如图所示,已知直线![]() 、
、![]() 相交于
相交于![]() ,
,![]() ,射线
,射线![]() 从
从![]() 位置起始,绕点
位置起始,绕点![]() 逆时针旋转,终边
逆时针旋转,终边![]() 与始边
与始边![]() 形成的角度为
形成的角度为![]() .
.
问题1:若![]() 逆时针旋转
逆时针旋转![]() 停止,则
停止,则
(1)![]() __________________时,
__________________时,![]() 平分
平分![]() ;
;
(2)![]() __________________时,
__________________时,![]() ;
;
(3)![]() __________________时,
__________________时,![]() ;
;
问题2:若![]() 逆时针旋转的速度为每秒
逆时针旋转的速度为每秒![]() ,在
,在![]() 匀速旋转的同时,直线
匀速旋转的同时,直线![]() 也从图的位置开始绕点
也从图的位置开始绕点![]() 逆时针匀速旋转,旋转速度为每秒
逆时针匀速旋转,旋转速度为每秒![]() ,当
,当![]() 完成旋转一周时,
完成旋转一周时,![]() 也同时停止旋转.设旋转时间为
也同时停止旋转.设旋转时间为![]() (
(![]() )秒.
)秒.
(1)旋转时间![]() 为多少时,射线
为多少时,射线![]() 与
与![]() 重合.请写出求解过程.
重合.请写出求解过程.
(2)观察旋转全过程,判断旋转时间![]() 为多少时,射线
为多少时,射线![]() 平分
平分![]() .请直接写出
.请直接写出![]() 的值.(注:
的值.(注:![]() 指大于
指大于![]() 且小于
且小于![]() 的角)
的角)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).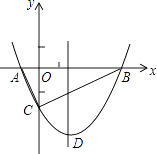
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6 000元,B型每台4 000元,C型每台2 500元,我市东坡中学计划将100 500元钱全部用于该电脑公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该校选择,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机抽取2000名学生进行调查,图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项)根据统计图提供的信息解决下列

问题:
(1)求图②中“科技类”所在扇形的圆心角α的度数
(2)该市2012年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市2014年共有50000名学生,请你估计该市2014年参加社团的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com