
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题:
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | |
一般 | ||
不好 | 36 |
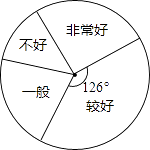
(1)本次抽样共调查了多少学生?
(2)补全统计表中所缺的数据.
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
【答案】
(1)解:较好的所占的比例是: ![]() ,
,
则本次抽样共调查的人数是:70÷ ![]() =200(人)
=200(人)
(2)解:
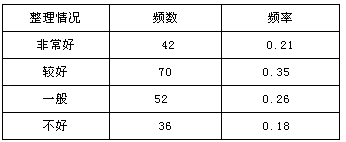
非常好的频数是:200×0.21=42(人),
一般的频数是:200﹣42﹣70﹣36=52(人),
较好的频率是: ![]() =0.35,
=0.35,
一般的频率是: ![]() =0.26,
=0.26,
不好的频率是: ![]() =0.18
=0.18
(3)解:该校学生整理错题集情况“非常好”和“较好”的学生一共约有1500×(0.21+0.35)=840(人)
(4)解:
![]()
则两次抽到的错题集都是“非常好”的概率是: ![]() =
= ![]()
【解析】(1)根据较好的部分对应的圆心角即可求得对应的百分比,即可求得总数,然后根据频率= ![]() 即可求解;(2)根据频率=
即可求解;(2)根据频率= ![]() 即可求解;(3)利用总人数乘以对应的频率即可;(4)利用树形图方法,利用概率公式即可求解.
即可求解;(3)利用总人数乘以对应的频率即可;(4)利用树形图方法,利用概率公式即可求解.
【考点精析】认真审题,首先需要了解扇形统计图(能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况),还要掌握列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数的概率.(请用“画树状图”或“列表”的方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的剧烈为碟高.
(1)抛物线y=x2对应的碟宽为;抛物线y= ![]() x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
(2)利用图(1)中的结论:抛物线y=ax2﹣4ax﹣ ![]() (a>0)对应的碟宽为6,求抛物线的解析式.
(a>0)对应的碟宽为6,求抛物线的解析式.
(3)将抛物线yn=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3,…),定义F1 , F2 , …..Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为 ![]() ,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
①求抛物线y2的表达式;
②若F1的碟高为h1 , F2的碟高为h2 , …Fn的碟高为hn . 则hn= , Fn的碟宽右端点横坐标为 . 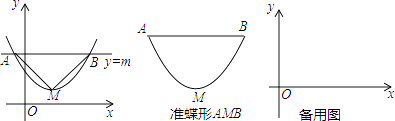
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )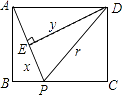
A.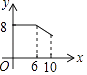
B.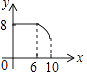
C.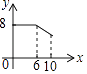
D.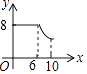
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点. 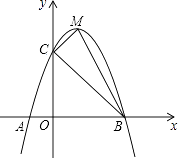
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(﹣4,0)、B(2,0)两点,与y轴交于点C,连接AC,BC.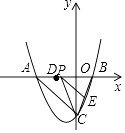
(1)求该抛物线的解析式;
(2)若点P是x轴上的一动点,且位于AB之间,过点P作PE∥AC,交BC于E,连接CP,设P点横坐标为x,△PCE的面积为S,请求出S关于x的解析式,并求△PCE面积的最大值;
(3)点为D(﹣2,0),若点M是线段AC上一动点,是否存在M点,能使△OMD是等腰三角形?若存在,请直接写出M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.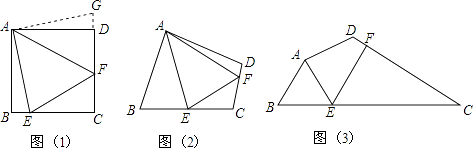
(1)【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图1证明上述结论.
(2)【类比引申】
如图2,四边形ABCD中∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD
(3)【探究应用】如图3,在某公园的同一水平面上,四条通道围成的ABCD,已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,且AE⊥AD,DF=40( ![]() ,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
,米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: ![]() =1.41,
=1.41, ![]() =1.73).
=1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,AC=2,BD=2 ![]() ,AC,BD相交于点O.
,AC,BD相交于点O. 
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G. ①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com