
【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点. 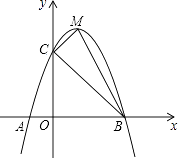
(1)求抛物线的解析式;
(2)求△MCB的面积;
(3)在抛物线上是否存在点P,使△PAB的面积等于△MCB的面积?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵A(﹣1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴ 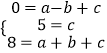 ,
,
解方程组,得 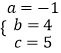 ,
,
故抛物线的解析式为y=﹣x2+4x+5
(2)解:过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积= ![]() MNOB.
MNOB.
∵y=﹣x2+4x+5=﹣(x﹣5)(x+1)=﹣(x﹣2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=﹣x+5,
当x=2时,y=﹣2+5=3,则N(2,3),
则MN=9﹣3=6,
则S△MCB= ![]() ×6×5=15
×6×5=15
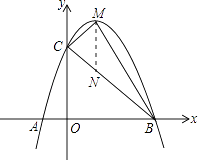
(3)解:在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(﹣1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴ ![]() ×6×|yP|=15,
×6×|yP|=15,
∴|yP|=5,yP=±5.
当yP=5时,﹣x2+4x+5=5,解得x1=0,x2=4;
当yP=﹣5时,﹣x2+4x+5=﹣5,解得x3=2+ ![]() ,x4=2﹣
,x4=2﹣ ![]() .
.
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+ ![]() ,﹣5),P3(2﹣
,﹣5),P3(2﹣ ![]() ,﹣5),使△PAB的面积等于△MCB的面积.
,﹣5),使△PAB的面积等于△MCB的面积.
【解析】(1)由A、C、D三点在抛物线上,根据待定系数法即可求出抛物线的解析式;(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积= ![]() MNOB;(3)先由△PAB的面积等于△MCB的面积,求出AB边上的高即点P的纵坐标的绝对值,再将点P的纵坐标代入抛物线的解析式,得到一元二次方程,如果方程有实数根,则在抛物线上存在点P,否则不存在.
MNOB;(3)先由△PAB的面积等于△MCB的面积,求出AB边上的高即点P的纵坐标的绝对值,再将点P的纵坐标代入抛物线的解析式,得到一元二次方程,如果方程有实数根,则在抛物线上存在点P,否则不存在.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系,请按要求完成下面的问题:
(1)以图中的点O为位似中心,将△ABC作位似变换且同向放大到原来的两倍,得到△A1B1C1;
(2)若△ABC内一点P的坐标为(a,b),则位似变化后对应的点P′的坐标是 . 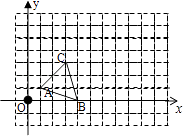
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点的坐标分别为(40,0)和(0,30),动点P从点A开始在线段AO上以每秒2个长度单位的速度向原点O运动、动直线EF从x轴开始以每1个单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于点E,F,连接EP,FP,设动点P与动直线EF同时出发,运动时间为t秒. 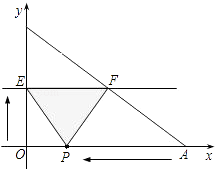
(1)求t=15时,△PEF的面积;
(2)直线EF、点P在运动过程中,是否存在这样的t,使得△PEF的面积等于160(平方单位)?若存在,请求出此时t的值;若不存在,请说明理由.
(3)当t为何值时,△EOP与△BOA相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | ﹣1 | 0 | m | 8 | … |
(1)可求得m的值为;
(2)求出这个二次函数的解析式;
(3)当y>3时,x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题:
整理情况 | 频数 | 频率 |
非常好 | 0.21 | |
较好 | 70 | |
一般 | ||
不好 | 36 |
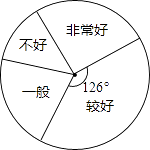
(1)本次抽样共调查了多少学生?
(2)补全统计表中所缺的数据.
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨
B.“抛一枚硬币正面朝上的概率为 ![]() ”表示每抛2次就有一次正面朝上
”表示每抛2次就有一次正面朝上
C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖
D.“抛一枚正方体骰子,朝上的点数为2的概率为 ![]() ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 ![]() 附近
附近
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4. 
(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出平面直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系,以B为位似中心,做△BA2C2 , 使△BA2C2与△ABC位似,且△BA2C2与△ABC位似比为2:1,并直接写出A2的坐标. 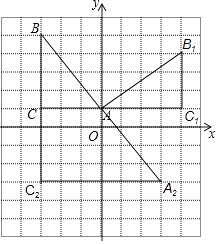
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com