练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，EF∥AD，∠1 =∠2，猜想∠BAC与∠DGA的关系，并说明理由。


      解：∠BAC + ∠DGA = 180°…………………1分

    理由：∵ EF∥AD

    ∴ ∠2 = ∠3  …………………………………………2分

    又∵ ∠1 = ∠2

    ∴ ∠1 = ∠3  ………………………………………4分

    ∴ AB∥DG   …………………………………………6分

    ∴ ∠BAC + ∠DGA = 180°…………………………8分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    函数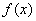在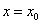处导数存在，若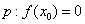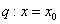；是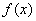的极值点，则（   ）

    A．是的充分必要条件      B. 是的充分条件，但不是的必要条件

    C. 是的必要条件，但不是的充分条件  D. 既不是的充分条件，也不是的必要条件

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，EF∥AD，∠1=∠2，∠BAC=65°．将下面求∠AGD的过程填写完整．

    解：∵EF∥AD（已知）

    ∴∠2=　　　　　　（　　　　　　）

    又∵∠1=∠2（已知）

    ∴∠1=　　　　　　（等量代换）

    ∴AB∥　　　　　　（　　　　　　）

    ∴∠BAC+　　　　　　=180°（　　　　　　）

    ∵∠BAC=65°（已知）

    ∴∠AGD=　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在实数﹣7.5，，4，，2π，0.15，中，有理数的个数为B，无理数的个数为A，则A﹣B的值为（　　）

    A．3       B．﹣3   C．1       D．﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，AB∥CD，EOF是直线AB、CD间的一条折线。

    （1）猜想∠1、∠2、∠3的数量关系，并说明理由。

    （2）如图2,将折一次改为折二次,若∠1=40°,∠2=60°,∠3=70°,则∠4=____。

    （3）如图3，若改为折多次，直接写出∠1，∠2，∠3，…，∠2n-1，∠2n之间的数量关系:____________________________________________________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示第1个图案是由黑白两种颜色的正六边形地面砖组成，第2个，第3个图案可以看作是第1个图案经过平移而得，那么第5个图案中有白色地面砖____块，第个图案中有白色地面砖的块数为______。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     (    )

        A.503.6        B.159.25      C.633.0       D.560

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，AB、CD相交于点O，∠A=∠1，∠B=∠2，则∠C=∠D．理由是：

    ∵∠A=∠1，∠B=∠2，（已知）

    且∠1=∠2（　　　　　　）

    ∴∠A=∠B．（等量代换）

    ∴AC∥BD（　　　　　　）．

    ∴∠C=∠D（　　　　　　）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，数轴上A、B两点表示的数分别为和5.1，则A、B两点之间表示整数的点共有（　　）

    A．6个  B．5个   C．4个  D．3个

    查看答案和解析>>

    同步练习册答案