
 如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.| CE |
| DE |
| 2 |
| 3 |
| CE |
| DE |
| 2 |
| 3 |
| DE2-AD2 |
| 2 |
| AD |
| AE |
| ||
| 4 |
| OC |
| CE |
| OC |
| 2k |
| AO2+AD2 |
| ||
|
| OA |
| OD |
| ||
| 3 |
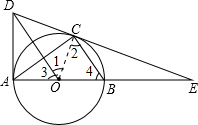 (1)证明:如图,连接OC.
(1)证明:如图,连接OC.
|
| CE |
| DE |
| 2 |
| 3 |
| DE2-AD2 |
| 2 |
| AD |
| AE |
| ||
| 4 |
| OC |
| CE |
| OC |
| 2k |
| ||
| 4 |
| OC |
| 2k |
| k | ||
|
| AO2+AD2 |
| ||
|
| OA |
| OD |
| ||
| 3 |


科目:初中数学 来源: 题型:
 2013年5月31日是第26个“国际无烟日”,这一天小敏与小伙伴们对人们“在娱乐场所吸烟”所持的三种态度(彻底禁烟、建立吸烟室、无所谓)进行调查,丙把调查结果绘制成了如图所示的扇形统计图,小红看了说这个图有问题,你认为( )
2013年5月31日是第26个“国际无烟日”,这一天小敏与小伙伴们对人们“在娱乐场所吸烟”所持的三种态度(彻底禁烟、建立吸烟室、无所谓)进行调查,丙把调查结果绘制成了如图所示的扇形统计图,小红看了说这个图有问题,你认为( )| A、没问题 |
| B、有问题,看不出调查了多少人 |
| C、有问题,赞成禁烟的还不够多 |
| D、有问题,所有百分数的和不等于1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,谢明住在一栋住宅楼AC上,他在家里的窗口点B处,看楼下一条公路的两侧点F和点E处(公路的宽为EF),测得俯角α、β分别为30°和60°,点F、E、C在同一直线上.
如图,谢明住在一栋住宅楼AC上,他在家里的窗口点B处,看楼下一条公路的两侧点F和点E处(公路的宽为EF),测得俯角α、β分别为30°和60°,点F、E、C在同一直线上.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,连接BP并延长,交直线l于点C,使得AB=AC.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O 上一点,连接BP并延长,交直线l于点C,使得AB=AC.| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
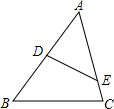 如图:在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,且AD:AC=2:3,那么DE:BC等于( )
如图:在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,且AD:AC=2:3,那么DE:BC等于( )| A、3:1 | B、1:3 |
| C、3:4 | D、2:3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com