练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．已知y=-（x-3）2+2，若点A（m，y1）、B（n，y2）（m＜n＜3）都在该抛物线上，则y1＜y2 （填＜、＞或=）

    分析 先判断函数的增减性，根据A、B的坐标可得出答案．

    解答 解：∵y=-（x-3）2+2，
    ∴抛物线对称轴为x=3，开口向下，
    ∴当x＜3时，y随x增大而增大，
    ∵m＜n＜3，
    ∴y1＜y2．
    故答案为：＜．

    点评 本题主要考查二次函数的增减性，根据二次函数解析式判断出增减性是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．已知点M（2，1）和点N（1，-2）在直线l：y=kx+b上，则直线l与x轴的交点坐标是（　　）
    A．（0，-5）B．（-5，0）C．（0，$\frac{5}{3}$）D．（$\frac{5}{3}$，0）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解方程组：
    （1）$\left\{\begin{array}{l}{\frac{x}{3}+\frac{y}{4}=1}\\{0.3x+0.4y=1.6}\end{array}\right.$；
    （2）$\left\{\begin{array}{l}{2x-3y-2=0}\\{\frac{2x-3y+5}{7}+2y=9}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列调查中适合采用抽样调查的是（　　）
    A．调查本班同学的视力
    B．调查一批节能灯管的使用寿命
    C．为保证“神舟9号”的成功发射，对其零部件进行检查
    D．对乘坐某班次客车的乘客进行安检

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．关于x的一元二次方程x2+nx+m=0的两根中有一个等于0，则m=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．我们已经研究了“圆周角”，并且知道圆周角的角度等于它所对弧的度数的一半，如图1，∠A=$\frac{\widehat{BC}的度数}{2}$．现将研究对象“顶点在圆上的角”改为“顶点在圆外的角”．定义：顶点在圆外，并且两边都和圆有公共点的角叫做圆外角，例如：图2，∠P为圆外角．


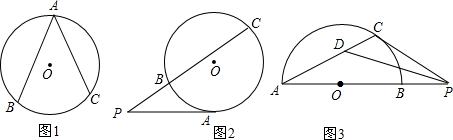
    ∠P=$\frac{\widehat{AmB}的度数-\widehat{AB}的度数}{2}$
    ∠P=$\frac{\widehat{AC}的度数-\widehat{AB}的度数}{2}$
    ∠P=$\frac{\widehat{CD}的度数-\widehat{AB}的度数}{2}$
    （1）如果以圆外角的两边与圆的公共点的个数作为分类标准，参照图2，请画出其它类型圆外角的示意图（要求：（请按需要选择下面的备用图，每一种类型画出一个示意图，标示相应字母，与图2同类型的不用再画）
    （2）如果圆外角所夹的两条弧的度数分别为α、β（α＞β），例如，图2中，圆外角∠P所夹的弧$\widehat{AC}$的度数为α，$\widehat{AB}$的度数为β，试结合你所画的图形探究∠P与α、β之间的数量关系，将发现的结论直接写在对应图形下方的横线上．
    （3）如图2，点P在⊙O外，PC边与⊙O相交于B，C两点，PA与⊙O相切于点A，所夹的弧$\widehat{AC}$，$\widehat{AB}$的度数分别为α、β（α＞β），求证：∠P=$\frac{1}{2}α-\frac{1}{2}β$．
    （4）如图3，AB为半圆直径，P为AB延长线上一个动点，过P作⊙O的切线，设切点为C，连接AC，作∠APC平分线交AC于D，猜想∠CDP的度数是否随点P在AB延长线上的位置的变化而变化？并对猜想加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．正方形ABCD的对角线交于点O，∠EOF=90°，且两边分别交直线AB于点E，交直线BC于点F，如图①有结论：BE+BF=$\frac{\sqrt{2}}{2}$AC．
    理由如下：∵四边形ABCD是正方形，∴OB=OC，∠EBO=∠FCO=45°，∠BOC=90°
    ∵∠EOF=90°，∴∠EOB=∠FOC，△EOB≌△FOC（ASA）∴BE=CF∵BC=CF+BF
    ∴BC=BE+BF∵四边形ABCD是正方形∴BC=$\frac{\sqrt{2}}{2}$AC，故BE-BF=$\frac{\sqrt{2}}{2}$AC．
    （1）将∠EOF旋转至图②、图③位置时，线段BE、BF与AC又有怎样的数量关系？请分别写出你的猜想并选择一种情况加以证明；
    （2）当AC=4$\sqrt{2}$，S△COF=1时，S△BOC=4，EF=$\sqrt{10}$或$\sqrt{26}$．

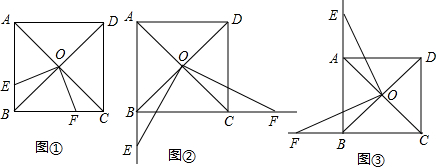
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．化简：$\frac{2ab+{a}^{2}}{{a}^{2}-{b}^{2}}$×$\frac{a-b}{a+2b}$=$\frac{a}{a+b}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列说法中，正确的是（　　）
    A．S=ab是代数式
    B．a，0，$\frac{2x}{3}$，$\frac{1}{x}$都是单项式
    C．单项式和多项式都是整式
    D．多项式a2-3ab+2b2是由a2，3ab，2b2组成

    查看答案和解析>>

    同步练习册答案