
分析 (1)先把方程组中的方程化为不含分母及小数的方程,再用加减消元法或代入消元法求解即可;
(2)把①变形为2x-3y=2,代入②求出y的值,进而可得出x的值.
解答 解:(1)原方程组可化为$\left\{\begin{array}{l}4x+2y=12①\\ 3x+4y=16②\end{array}\right.$,
①×2-②得,5x=8,解得x=$\frac{8}{5}$,
把x的值代入①得,$\frac{32}{5}$+2y=12,解得y=$\frac{14}{5}$.
故方程组的解为$\left\{\begin{array}{l}x=\frac{8}{5}\\ y=\frac{14}{5}\end{array}\right.$;
(2)$\left\{\begin{array}{l}2x-3y-2=0①\\ \frac{2x-3y+5}{7}+2y=9②\end{array}\right.$,
由①得2x-3y=2,
代入②得$\frac{2+5}{7}$+2y=9,解得y=4,
把y=4代入①得,2x-12-2=0,解得x=7.
故方程组的解为$\left\{\begin{array}{l}x=7\\ y=4\end{array}\right.$.
点评 本题考查的是解二元一次方程组,熟知解二元一次方程组的加减消元法和代入消元法是解答此题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 近似数3.20与3.2的精确度一样 | |
| B. | 近似数3.0×103与3000的意义完全一样 | |
| C. | 0.37万与3.2×103精确度不一样 | |
| D. | 3.36万精确到百位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,C为线段AB上的一点,D为线段AC的中点,E为线段CB的中点,AB=9cm,求DE的长.(请将解答内容补充完整)
如图所示,C为线段AB上的一点,D为线段AC的中点,E为线段CB的中点,AB=9cm,求DE的长.(请将解答内容补充完整)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
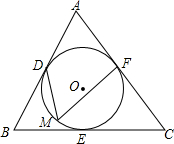 如图,⊙O分别切△ABC的边AB、BC、CA于点D、E、F,∠B=70°,∠C=60°,M是$\widehat{DEF}$上的动点(与点D、E不重合),∠DMF的大小一定吗?若一定,求∠DMF的度数;若不一定,请说明理由.
如图,⊙O分别切△ABC的边AB、BC、CA于点D、E、F,∠B=70°,∠C=60°,M是$\widehat{DEF}$上的动点(与点D、E不重合),∠DMF的大小一定吗?若一定,求∠DMF的度数;若不一定,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com