

·ЦОц ЈЁ1Ј©ЧчDHЎНBCЈ¬ёщѕЭТСЦЄМхјюЗуµГDH=HC=4Ј¬Ѕш¶шµГіцFH=8Ј¬И»єуёщѕЭGMЎОDHЈ¬µГіцЎа$\frac{FM}{FH}$=$\frac{GM}{DH}$Ј¬јґ$\frac{2}{4}$=$\frac{t+2}{8}$Ј¬јґїЙЗуµГtµДЦµЈ»
ЈЁ2Ј©·ЦЛДЦЦЗйїц·Ц±рМЦВЫЗуµГјґїЙЈ»
ЈЁ3Ј©ЧчNKЎНBCЈ¬ёщѕЭNKЎОDHЈ¬µГіц$\frac{NK}{DH}$=$\frac{FK}{FH}$Ј¬ЙиNK=KR=xЈ¬ФтFK=t+4-xЈ¬Фт$\frac{x}{4}$=$\frac{t+4-x}{8}$Ј¬ЗуµГx=$\frac{t+4}{3}$Ј¬µГіцFK=$\frac{2}{3}$ЈЁt+4Ј©Ј¬УЪADЎОCFЈ¬µГіцЎПF=ЎПQDNЈ¬ЛщТФУРБЅЦЦЗйїцµДЦ±ЅЗИэЅЗРОЈ¬И»єу·Ц±рМЦВЫЗуµГјґїЙЈ®
Ѕвґр 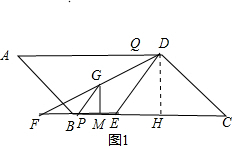 ЅвЈєЈЁ1Ј©ИзНј1Ј¬µгGФЪПЯ¶ОDEЙПК±Ј¬FP=tЈ¬FM=t+2Ј¬
ЅвЈєЈЁ1Ј©ИзНј1Ј¬µгGФЪПЯ¶ОDEЙПК±Ј¬FP=tЈ¬FM=t+2Ј¬
ЧчDHЎНBCЈ¬
ЎЯФЪЖЅРРЛД±ЯРОABCDЦРЈ¬ЎПABC=135ЎгЈ¬
ЎаЎПC=45ЎгЈ¬
ЎаЎчDHCКЗµИСьЦ±ЅЗИэЅЗРОЈ¬
ЎЯDC=AB=4$\sqrt{2}$Ј¬
ЎаDH=HC=4Ј¬
ЎЯBC=AD=10Ј¬BF=2Ј¬
ЎаFC=12Ј¬
ЎаFH=8Ј¬
ЎЯGMЎОDHЈ¬
Ўа$\frac{FM}{FH}$=$\frac{GM}{DH}$Ј¬јґ$\frac{2}{4}$=$\frac{t+2}{8}$Ј¬
ЅвµГt=2Ј»
ЈЁ2Ј©ўЩµ±0ЎЬtЈј2К±Ј¬ИзНј2Ј¬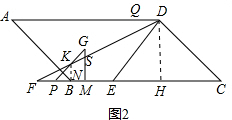
ЧчKNЎНBCУЪNЈ¬
ЎЯDHЎНBCЈ¬
ЎаKNЎОDHЈ¬
Ўа$\frac{KN}{DH}$=$\frac{FB}{FH}$Ј¬
ЙиKN=PN=xЈ¬ФтFN=t+xЈ¬
Ўа$\frac{x}{4}$=$\frac{x+t}{8}$Ј¬
Ўаx=tЈ¬
ЎаKN=PN=tЈ¬
ЎаFN=2tЈ¬
ЎаMN=t+2-2t=2-tЈ¬
ЎЯKNЎОGMЈ¬
Ўа$\frac{KN}{MS}$=$\frac{FN}{FM}$Ј¬јґ$\frac{t}{MS}$=$\frac{2t}{t+2}$Ј¬
ЎаMS=$\frac{t+2}{2}$Ј¬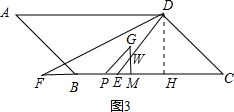
ЎаGS=2-$\frac{t+2}{2}$=$\frac{2-t}{2}$Ј¬
ЎаS=SЎчPMG-SЎчKGS=$\frac{1}{2}$ЎБ2ЎБ2-$\frac{1}{2}$ЎБ$\frac{2-t}{2}$ЎБЈЁ2-tЈ©=-$\frac{1}{4}$t2+t+1ЈЁ0ЈјtЈј2Ј©Ј»
ўЪµ±2ЎЬtЎЬ3К±Ј¬ИзНј1Ј¬S=$\frac{1}{2}$ЎБ2ЎБ2=2Ј¬
ўЫµ±3ЈјtЎЬ4.5К±Ј¬ИзНј3Ј¬
ЎЯFM=t+2Ј¬EF=3+2=5Ј¬EH=10-3-4=3Ј¬
ЎаEM=t+2-5=t-3Ј¬
ЎЯGMЎОDHЈ¬
Ўа$\frac{WM}{DH}$=$\frac{EM}{EH}$Ј¬јґ$\frac{WM}{4}$=$\frac{t-3}{3}$Ј¬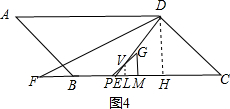
ЎаWM=$\frac{4}{3}$ЈЁt-3Ј©Ј¬
ЎаS=SЎчPMG-SЎчEMW=2-$\frac{1}{2}$ЈЁt-3Ј©ЎБ$\frac{4}{3}$ЈЁt-3Ј©=-$\frac{2}{3}$t2+4t-4Ј»
ўЬµ±4.5ЈјtЎЬ5К±Ј¬ИзНј4Ј¬ЧчVLЎНBCЈ¬ФтЎчPVLКЗµИСьЦ±ЅЗИэЅЗРОЈ¬
ЎаVL=PLЈ¬
ЙиPL=VL=xЈ¬ФтEL=t+x-5
ЎЯVLЎОDHЈ¬
Ўа$\frac{VL}{DH}$=$\frac{EL}{EH}$Ј¬
Ўа$\frac{x}{4}$=$\frac{t+x-5}{3}$Ј¬
Ўаx=20-4tЈ¬
ЎаVL=20-4tЈ¬
ЎЯPE=5-tЈ¬
ЎаS=$\frac{1}{2}$PE•VL=$\frac{1}{2}$ЈЁ5-tЈ©ЈЁ20-4tЈ©=2t2-20t+50
ЧЫЙПЈ¬SУлtЦ®јдµДєЇКэ№ШПµКЅОЄЈєS=$\left\{\begin{array}{l}{-\frac{1}{4}{t}^{2}+t+1ЈЁ0ЎЬtЈј2Ј©}\\{2ЈЁ2ЎЬtЎЬ3Ј©}\\{-\frac{2}{3}{t}^{2}+4t-4ЈЁ3ЈјtЎЬ4.5Ј©}\\{2{t}^{2}-20t+50ЈЁ4.5ЈјtЎЬ5Ј©}\end{array}\right.$Ј»
ЈЁ3Ј©ИзНј5Ј¬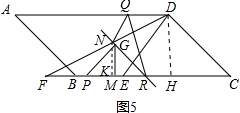 ЧчNKЎНBCЈ¬
ЧчNKЎНBCЈ¬
ЎаNKЎОDHЈ¬
Ўа$\frac{NK}{DH}$=$\frac{FK}{FH}$Ј¬
ЎЯPF=tЈ¬PM=MR=2Ј¬
ЎаFR=t+4Ј¬
ЙиNK=KR=xЈ¬ФтFK=t+4-xЈ¬
ЎЯFH=8Ј¬DH=4Ј¬
Ўа$\frac{x}{4}$=$\frac{t+4-x}{8}$Ј¬
Ўаx=$\frac{t+4}{3}$Ј¬
ЎаFK=$\frac{2}{3}$ЈЁt+4Ј©Ј¬
ЎЯADЎОCFЈ¬
ЎаЎПF=ЎПQDNЈ¬
ўЩµ±ЎПDQN=90ЎгК±Ј¬QЎўNЎўKИэµг№ІПЯЈ¬
ЎаQN=DH-NK=4-$\frac{t+4}{3}$=$\frac{8-t}{3}$Ј¬
ЎаЎчKFNЎЧЎчQDNЈ¬
Ўа$\frac{DQ}{FK}$=$\frac{QN}{NK}$Ј¬
ЎЯFK=t+4-$\frac{t+4}{3}$=$\frac{2t+8}{3}$Ј¬
Ўа$\frac{t}{\frac{2t+8}{3}}$=$\frac{\frac{8-t}{3}}{\frac{t+4}{3}}$Ј¬ЅвµГt=$\frac{16}{5}$Ј¬
ўЪµ±ЎПDNQ=90ЎгК±Ј¬
ЎаЎчKFNЎЧЎчNDQЈ¬
Ўа$\frac{DQ}{FN}$=$\frac{DN}{FK}$Ј¬
ЎЯFH=8Ј¬DH=4Ј¬
ЎаFD=4$\sqrt{5}$
ЎЯNKЎОDHЈ¬
Ўа$\frac{FN}{FD}$=$\frac{NK}{DH}$Ј¬
Ўа$\frac{FN}{4\sqrt{5}}$=$\frac{\frac{t+4}{3}}{4}$Ј¬
ЎаFN=$\frac{\sqrt{5}}{3}$ЈЁt+4Ј©Ј¬
ЎаDN=4$\sqrt{5}$-$\frac{\sqrt{5}}{3}$ЈЁt+4Ј©=$\frac{\sqrt{5}}{3}$ЈЁ8-tЈ©Ј¬
Ўа$\frac{t}{\frac{\sqrt{5}}{3}ЈЁt+4Ј©}$=$\frac{\frac{\sqrt{5}}{3}ЈЁ8-tЈ©}{\frac{2}{3}ЈЁt+4Ј©}$
ЅвµГt=$\frac{40}{11}$Ј¬
ЧЫЙПЈ¬ФЪХыёцФЛ¶Ї№эіМЦРЈ¬ґжФЪµгQЈ¬К№ЎчQRNКЗЦ±ЅЗИэЅЗРОЈ¬ґЛК±tОЄ$\frac{16}{5}$»т$\frac{40}{11}$Ј®
µгЖА ±ѕМвїјІйБЛЖЅРРПЯ·ЦПЯ¶ОіЙ±ИАэ¶ЁАнЈ¬ИэЅЗРОПаЛЖµДЕР¶ЁєНРФЦКЈ¬№ґ№Й¶ЁАнµДУ¦УГЈ¬ТФј°ИэЅЗРОГж»эµИЈ¬·ЦАаМЦВЫЛјПлµДФЛУГКЗЅвМвµД№ШјьЈ®


 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | 1ёц | BЈ® | 2ёц | CЈ® | 3ёц | DЈ® | 4ёц |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | µчІй±ѕ°аН¬С§µДКУБ¦ | |
| BЈ® | µчІйТ»ЕъЅЪДЬµЖ№ЬµДК№УГКЩГь | |
| CЈ® | ОЄ±ЈЦ¤Ў°ЙсЦЫ9єЕЎ±µДіЙ№¦·ўЙдЈ¬¶ФЖдБгІїјюЅшРРјмІй | |
| DЈ® | ¶ФіЛЧшДі°аґОїНіµµДіЛїНЅшРР°Іјм |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
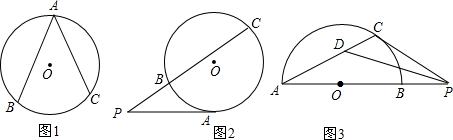
 ЎПP=$\frac{\widehat{AmB}µД¶ИКэ-\widehat{AB}µД¶ИКэ}{2}$ |  ЎПP=$\frac{\widehat{AC}µД¶ИКэ-\widehat{AB}µД¶ИКэ}{2}$ |  ЎПP=$\frac{\widehat{CD}µД¶ИКэ-\widehat{AB}µД¶ИКэ}{2}$ |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com