Question

5．如图，在正方形ABCD中，AB=4，BD是对角线．将△DCB绕着D点逆时针旋转α（90°＜α＜180°），得到△DEF，连接BF，CE相交于G点，EG=1，则BF=$\sqrt{62}$+$\sqrt{2}$．

Answer 1

分析 作EH⊥BF于H，连接DG，CE交BD于O．首先证明DG⊥BF，推出FG=BG，求出FG即可解决问题．

解答 解：作EH⊥BF于H，连接DG，CE交BD于O．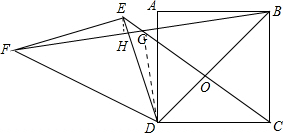

∵∠EDC=90°+∠ADE，∠BDF=90°+∠ADE，
∴∠EDC=∠FDB，
∵DF=DB，CD=DE，
∴∠DFB=∠DBF=∠DCE=∠DEC，
∵∠BOG=∠DOC，
∴△BOG∽△COD，
∴$\frac{OG}{OD}$=$\frac{OB}{OC}$，∠ODC=∠OGB=45°
∴$\frac{OG}{OB}$=$\frac{OD}{OC}$，
∴△GOD∽△BOC，
∴∠DGO=∠OBC=45°，
∴∠DGB=90°，
∵DF=DB，
∴FG=BG，
在Rt△EHG中，∵∠EGH=∠BGO=45°，EG=1，
∴EH=HG=$\frac{\sqrt{2}}{2}$，
在Rt△EFH中，∵EF=4，EH=$\frac{\sqrt{2}}{2}$，
∴FH=$\sqrt{E{F}^{2}-E{H}^{2}}$=$\frac{\sqrt{62}}{2}$，
∴FG=BG=$\frac{\sqrt{62}+\sqrt{2}}{2}$，
∴BF=$\sqrt{62}$+$\sqrt{2}$．
故答案为$\sqrt{62}$+$\sqrt{2}$．

点评 本题考查正方形的性质、相似三角形的判定和性质、等腰三角形的性质、勾股定理的等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考填空题中的压轴题．